Informationen zum Buch
Rekursion und rekursive Funktionen
Definition
Die Rekursion hat etwas mit Unendlichkeit zu tun. Ich weiß, dass die Rekursion etwas mit Unendlichkeit zu tun hat.
Ich denke, ich weiß, dass die Rekursion etwas mit Unendlichkeit zu tun hat. Er ist sicher, dass ich denke, ich
weiß, dass die Rekursion etwas mit Unendlichkeit zu tun hat. Wir zweifeln, ob er sicher ist, dass ich denke, ich
weiß, dass die Rekursion etwas mit Unendlichkeit zu tun hat. ...
Jedem wird wohl klar sein, dass wir dieses sprachliche Spiel beliebig fortsetzen können. Dies ist ein Beipiel für Rekursion in der natürlichen Sprache. Die Rekursion ist nicht nur eine fundamentale Eigenschaft der natürlichen Sprache, sondern
der menschlichen kognitiven Fähigkeiten. Unser ganzes Denken basiert auf rekursiven Denkprozessen. Der Linguist
Noam Chomsky hatte einen Formalismus eingeführt, um sprachliche Ausdrücke mit Hilfe einer Metasprache formal zu definieren.
Diese Definition definiert rekursiv eine Grammatik. Diese formalen Sprachen von Chomsky werden auch zur Definition und Spezifikation von Programmiersprachen in der Informatik benutzt. Die Vollständige Induktion in der Mathematik ist auch eine
Form von Rekursion.
Aber wir wollen nicht Rekursion im allgemeinen oder in der natürlichen Sprache beschreiben, sondern uns geht es um rekursive Funktionen in der Programmiersprache Python.
Das Adjektiv "rekursiv" stammt vom lateinischen Verb "recurrere", was "zurücklaufen" bedeutet. Das ist genau das,
was eine rekursive Definition oder eine rekursive Funktion macht: Sie läuft gewissermaßen zurück auf sich selbst, indem
sie sich selbst wieder aufruft. Die meisten von denen, die sich bereits ein wenig mit Mathematik oder Informatik
beschäftigt haben, wird bereits die Fakultät begegnet sein. Sie ist meist das Standardbeispiel für Rekursion in jedem Buch zum Erlernen einer Programmiersprache. Mathematisch wird sie wie folgt definiert:
n! = n * (n-1)!, if n > 1 and f(1) = 1
Definition der Rekursion
Die Rekursion ist eine Programmiertechnik oder Programmierkonzept, indem eine Funktion sich selbst ein oder mehrmals in ihrem Funktionskörper (body) aufruft. Eine Funktionsdefinition, die die Bedingungen der Rekursion erfüllt, nennen wir eine rekursive Funktion.Abbruchbedingung:
Eine rekursive Funktion muss terminieren, damit man sie in einem Programm benutzen kann. Eine rekursive Funktion terminiert, wenn mit jedem Rekursionsschritt das Problem reduziert wird und sich in Richtung der Abbruchbedingung, d.h. dem Fall, in dem die Funktion sich nicht mehr selbst aufruft. So liefert beispielweise die Fakultätsfunktion für das Argument 1 den Wert 1 zurück, ohne dass ein rekursiver Aufruf notwendig ist. (Anmerkung für Mathematiker: Das Abbruchkriterium in einer rekursiven Funktion entspricht der Induktionsverankerung bei der vollständigen Induktion!)
Eine rekursive Funktion kann in eine Endlosschleife führen, wenn das Abbruchkriterium nicht erreicht wird.
Beispiel für die Fakultät:
4! = 4 * 3!
3! = 3 * 2!
2! = 2 * 1
Ersetzt man die ausgerechneten Werte in der jeweiligen Ursprungsgleichung, erhält man für 4! folgenden Ausdruck:
4! = 4 * 3 * 2 * 1
Ganz allgemein könnten wir sagen: Rekursion ist eine Methode in der Informatik, in der die Lösung für ein Problem auf die Lösung kleinerer Instanzen des Problems zurückgeführt wird.
Rekursive Funktionen in Python
Als Beispiel für eine rekursive Funktion in Python wählen wir eine rekursive Implementierung der Fakultätsfunktion in Python. Man sieht, dass das Pythonskript ebenso elegant wie die mathematische Funktion ist:
def factorial(n):
if n == 1:
return 1
else:
return n * factorial(n-1)
Wenn wir nachvollziehen wollen, wie die Funktion funktioniert, können wir zwei print()-Funktionen ergänzen:
def factorial(n):
print("factorial has been called with n = " + str(n))
if n == 1:
return 1
else:
res = n * factorial(n-1)
print("intermediate result for ", n, " * factorial(" ,n-1, "): ",res)
return res
print(factorial(5))
Obiges Python-Skript liefert folgende Ausgaben:
factorial has been called with n = 5 factorial has been called with n = 4 factorial has been called with n = 3 factorial has been called with n = 2 factorial has been called with n = 1 intermediate result for 2 * factorial( 1 ): 2 intermediate result for 3 * factorial( 2 ): 6 intermediate result for 4 * factorial( 3 ): 24 intermediate result for 5 * factorial( 4 ): 120 120Die Fakultätsfunktion lässt sich natürlich auch iterativ schreiben:
def iterative_factorial(n):
result = 1
for i in range(2,n+1):
result *= i
return result
Die Tücken der Rekursion
In diesem Unterkapitel von unserem Tutorial geht es um ein spezielles Problem bei der Rekursion. Ruft eine
Funktion sich in einem Ausdruck wiederholt auf, erhalten wir ein exponentielles Laufzeitverhalten.
Am Beispiel der Fibonacci-Zahlen demonstrieren wir, wie dieses exponentielle Laufzeitverhalten zustande kommt.
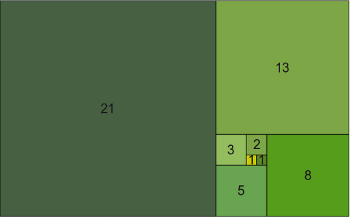
Die Fibonacci-Zahlen sind eine unendliche Zahlenfolge. Deshalb werden die Fibonacci-Zahlen auch als Fibonacci-Folge bezeichnet.
Aufgabe:
Im folgenden sehen sie die ersten Glieder der Fibonacci-Folge. Versuchen sie doch einmal das Konstruktionsprinzip dieser Folge zu erkennen:
0,1,1,2,3,5,8,13,21,34,55,89, ...
Es sollte hoffentlich nicht zu schwer gewesen sein. Jede Zahl, außer den beiden ersten, ergibt sich aus der Summe der beiden Vorgänger.
Formale Definition der Fibonacci-Zahlen:
Fn = Fn-1 + Fn-2
with
F0 = 0
and F1 = 1
Die Fibonacci-Zahlen sind nach dem Mathematiker Leonardo von Pisa, besser bekannt als Fibonacci, benannt. In seinem Buch "Liber Abaci", das im Jahre 1202 veröffentlicht wurde, führte er diese Folge als Übungsaufgabe ein. In dieser Übung geht es um Kaninchen. Seine Folge beginnt mit F1 = 1, während in modernen Mathematikbüchern und Büchern über Programmiersprachen die Folge meistens mit dem Wert für das Argument 0 startet, also F0 = 0. Dies ist aber gewissermaßen nur Geschmackssache, denn ob man bei 0 oder 1 startet hat keine Auswirkungen auf die weiteren Folgeglieder.
Die Fibonacci-Zahlen resultieren also aus einem "künstlichen" Kaninchenproblem, das die folgenden Bedingungen erfüllt:
- Die Anfangspopulation wird von einem Kaninchenpaar gebildet
- Ein neuegeborenes Kaninchenpaar kann sich erst am Ende des ersten Monats paaren und wirft am Ende des zweiten Monates ein weiteres Paar.
- Ansonsten wirft jedes Kaninchenpaar jeweils ein weiteres Kaninchenpaar pro Monat.
- Sie sind unsterblich
Fibonacci_Folge in Python
Nun kommen wir endlich wieder zu Python und den rekursiven Funktionen zurück. Die Fibonacci-Zahlen lassen sich sehr leicht als rekursive Python-Funktion realisieren. Diese spiegelt ziemlich exakt die rekursive mathematische Funktion:
def fib(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
Eine iterative Funktion zur Berechnung der Fibonacci Zahlen lässt sich ebenso leicht in Python bewerkstelligen,
wie wir im folgenden Skript sehen können:
def fibi(n):
a, b = 0, 1
for i in range(n):
a, b = b, a + b
return a
Benutzt man die beiden Funktionen fib() und fibi() stellt man sehr schnell fest, dass sie ein deutlich unterschiedliches Laufzeitverhalten an den Tag legen. Bei kleinen Werten z.B. n = 10, 11 oder 15 hat man rein Gefühlsmäßig, also ohne exakte Zeitmessung das Gefühl, dass fibi() und fib() genauso schnell wären. Aber bei Werten ab n = 30 sieht es deutlich anders aus. fib() braucht nun sekundenlang, während fibi() weiterhin "sofort" mit dem Ergebnis da ist. Um dieses Gefühl mit soliden
Messwerten zu untermauern, haben wir ein Skript geschrieben, mit dem wir die Zeiten messen können:
from timeit import Timer
from fibo import fib
t1 = Timer("fib(10)","from fibo import fib")
for i in range(1,41):
s = "fib(" + str(i) + ")"
t1 = Timer(s,"from fibo import fib")
time1 = t1.timeit(3)
s = "fibi(" + str(i) + ")"
t2 = Timer(s,"from fibo import fibi")
time2 = t2.timeit(3)
print("n=%2d, fib: %8.6f, fibi: %7.6f, percent: %10.2f" % (i, time1, time2, time1/time2))
time1 ist die Zeit in Sekunden, die drei Aufrufe von fib(n) benötigen und time2 ist entsprechend die Zeit für drei
Aufrufe der iterativen Funktion fibi(). Wenn wir uns die Ergebnisse anschauen, sehen wir, dass fib(20) etwa 14 Millisekunden
benötigt, während fibi(20) für drei Aufrufe gerade 0,011 Millisekunden benötigt. fibi(20) ist also etwa 1300 Mal schneller als fib(20).
fib(40) braucht bereits 215 Sekunden, also mehr als 3,5 Minuten, während fibi(4) sich mit 0,016 Millisekunden begnügt.
n= 1, fib: 0.000004, fibi: 0.000005, percent: 0.81 n= 2, fib: 0.000005, fibi: 0.000005, percent: 1.00 n= 3, fib: 0.000006, fibi: 0.000006, percent: 1.00 n= 4, fib: 0.000008, fibi: 0.000005, percent: 1.62 n= 5, fib: 0.000013, fibi: 0.000006, percent: 2.20 n= 6, fib: 0.000020, fibi: 0.000006, percent: 3.36 n= 7, fib: 0.000030, fibi: 0.000006, percent: 5.04 n= 8, fib: 0.000047, fibi: 0.000008, percent: 5.79 n= 9, fib: 0.000075, fibi: 0.000007, percent: 10.50 n=10, fib: 0.000118, fibi: 0.000007, percent: 16.50 n=11, fib: 0.000198, fibi: 0.000007, percent: 27.70 n=12, fib: 0.000287, fibi: 0.000007, percent: 41.52 n=13, fib: 0.000480, fibi: 0.000007, percent: 69.45 n=14, fib: 0.000780, fibi: 0.000007, percent: 112.83 n=15, fib: 0.001279, fibi: 0.000008, percent: 162.55 n=16, fib: 0.002059, fibi: 0.000009, percent: 233.41 n=17, fib: 0.003439, fibi: 0.000011, percent: 313.59 n=18, fib: 0.005794, fibi: 0.000012, percent: 486.04 n=19, fib: 0.009219, fibi: 0.000011, percent: 840.59 n=20, fib: 0.014366, fibi: 0.000011, percent: 1309.89 n=21, fib: 0.023137, fibi: 0.000013, percent: 1764.42 n=22, fib: 0.036963, fibi: 0.000013, percent: 2818.80 n=23, fib: 0.060626, fibi: 0.000012, percent: 4985.96 n=24, fib: 0.097643, fibi: 0.000013, percent: 7584.17 n=25, fib: 0.157224, fibi: 0.000013, percent: 11989.91 n=26, fib: 0.253764, fibi: 0.000013, percent: 19352.05 n=27, fib: 0.411353, fibi: 0.000012, percent: 34506.80 n=28, fib: 0.673918, fibi: 0.000014, percent: 47908.76 n=29, fib: 1.086484, fibi: 0.000015, percent: 72334.03 n=30, fib: 1.742688, fibi: 0.000014, percent: 123887.51 n=31, fib: 2.861763, fibi: 0.000014, percent: 203442.44 n=32, fib: 4.648224, fibi: 0.000015, percent: 309461.33 n=33, fib: 7.339578, fibi: 0.000014, percent: 521769.86 n=34, fib: 11.980462, fibi: 0.000014, percent: 851689.83 n=35, fib: 19.426206, fibi: 0.000016, percent: 1216110.64 n=36, fib: 30.840097, fibi: 0.000015, percent: 2053218.13 n=37, fib: 50.519086, fibi: 0.000016, percent: 3116064.78 n=38, fib: 81.822418, fibi: 0.000015, percent: 5447430.08 n=39, fib: 132.030006, fibi: 0.000018, percent: 7383653.09 n=40, fib: 215.091484, fibi: 0.000016, percent: 13465060.78
Was ist faul an unserer rekursiven Implementierung?
Schauen wir uns den Berechnungsbaum an, d.h. die Reihenfolge, in der die Funktionaufrufe erfolgen. Statt fib() schreiben wir allerdings vereinfachend f().
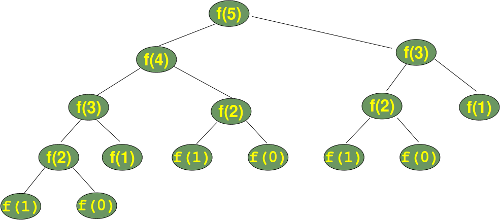
Wir können sehen, dass der Unterbaum zur Berechnung von f(2) (also fib(3)) drei Mal auftaucht und der Unterbaum zur Berechnung von f(3) zweimal. Wenn man sich vorstellt, f(6) zu berechnen, erkennt man, dass f(4) zweimal aufgerufen wird, f(3) dreimal und so weiter. Das bedeutet, dass alle Berechnungen immer wieder durchgeführt werden, da bereits berechnete Werte nicht gespeichert werden. Sie müssen also immer wieder aufs Neue berechnet werden.
Wir können eine "Erinnerung" für unsere rekursive Version implementieren. Dazu nutzen wir ein Dictionary, in dem wir bereits berechnete Werte speichern:
memo = {0:0, 1:1}
def fibm(n):
if not n in memo:
memo[n] = fibm(n-1) + fibm(n-2)
return memo[n]
Wir schauen uns wieder die benötigten Zeiten im Vergleich zu fibi() an:
from timeit import Timer
from fibo import fib
t1 = Timer("fib(10)","from fibo import fib")
for i in range(1,41):
s = "fibm(" + str(i) + ")"
t1 = Timer(s,"from fibo import fibm")
time1 = t1.timeit(3)
s = "fibi(" + str(i) + ")"
t2 = Timer(s,"from fibo import fibi")
time2 = t2.timeit(3)
print("n=%2d, fib: %8.6f, fibi: %7.6f, percent: %10.2f" % (i, time1, time2, time1/time2))
Wir können sehen, dass unsere neue Funktionsversion sogar schneller ist als die iterative. Insbesondere die großen Argumente haben einen besonderen Vorteil von der Memoisation:
n= 1, fib: 0.000011, fibi: 0.000015, percent: 0.73 n= 2, fib: 0.000011, fibi: 0.000013, percent: 0.85 n= 3, fib: 0.000012, fibi: 0.000014, percent: 0.86 n= 4, fib: 0.000012, fibi: 0.000015, percent: 0.79 n= 5, fib: 0.000012, fibi: 0.000016, percent: 0.75 n= 6, fib: 0.000011, fibi: 0.000017, percent: 0.65 n= 7, fib: 0.000012, fibi: 0.000017, percent: 0.72 n= 8, fib: 0.000011, fibi: 0.000018, percent: 0.61 n= 9, fib: 0.000011, fibi: 0.000018, percent: 0.61 n=10, fib: 0.000010, fibi: 0.000020, percent: 0.50 n=11, fib: 0.000011, fibi: 0.000020, percent: 0.55 n=12, fib: 0.000004, fibi: 0.000007, percent: 0.59 n=13, fib: 0.000004, fibi: 0.000007, percent: 0.57 n=14, fib: 0.000004, fibi: 0.000008, percent: 0.52 n=15, fib: 0.000004, fibi: 0.000008, percent: 0.50 n=16, fib: 0.000003, fibi: 0.000008, percent: 0.39 n=17, fib: 0.000004, fibi: 0.000009, percent: 0.45 n=18, fib: 0.000004, fibi: 0.000009, percent: 0.45 n=19, fib: 0.000004, fibi: 0.000009, percent: 0.45 n=20, fib: 0.000003, fibi: 0.000010, percent: 0.29 n=21, fib: 0.000004, fibi: 0.000009, percent: 0.45 n=22, fib: 0.000004, fibi: 0.000010, percent: 0.40 n=23, fib: 0.000004, fibi: 0.000010, percent: 0.40 n=24, fib: 0.000004, fibi: 0.000011, percent: 0.35 n=25, fib: 0.000004, fibi: 0.000012, percent: 0.33 n=26, fib: 0.000004, fibi: 0.000011, percent: 0.34 n=27, fib: 0.000004, fibi: 0.000011, percent: 0.35 n=28, fib: 0.000004, fibi: 0.000012, percent: 0.32 n=29, fib: 0.000004, fibi: 0.000012, percent: 0.33 n=30, fib: 0.000004, fibi: 0.000013, percent: 0.31 n=31, fib: 0.000004, fibi: 0.000012, percent: 0.34 n=32, fib: 0.000004, fibi: 0.000012, percent: 0.33 n=33, fib: 0.000004, fibi: 0.000013, percent: 0.30 n=34, fib: 0.000004, fibi: 0.000012, percent: 0.34 n=35, fib: 0.000004, fibi: 0.000013, percent: 0.31 n=36, fib: 0.000004, fibi: 0.000013, percent: 0.31 n=37, fib: 0.000004, fibi: 0.000014, percent: 0.29 n=38, fib: 0.000004, fibi: 0.000014, percent: 0.29 n=39, fib: 0.000004, fibi: 0.000013, percent: 0.31 n=40, fib: 0.000004, fibi: 0.000014, percent: 0.29
Übungen
- Schreibe eine rekursive Version der Funktion f(n) = 3 * n, also eine Funktion, die die Vielfachen von 3 berechnet
- Schreibe eine rekursive Python-Funktion, welche die Summe der ersten
nganzen Zahlen zurückliefert.
(Hinweis: Diese Funktion sieht ähnlich wie die Fakultätsfunktion aus! - Schreibe eine Funktion, die das Pascalsche Dreick implementiert:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
Lösungen zu den Übungen:
-
Lösung zu unseren ersten Übung zur Rekursion:
Mathematisch können wir es wie folgt formulieren:
f(1) = 3,
f(n+1) = f(n) + 3
Die Funktion in Python:def mult3(n): if n == 1: return 3 else: return mult3(n-1) + 3 for i in range(1,10): print(mult3(i)) -
Lösung zur zweiten Übung:
def sum_n(n): if n== 0: return 0 else: return n + sum_n(n-1) -
Python-Programm zur Berechnung des Pacalschen Dreiecks:
def pascal(n): if n == 1: return [1] else: line = [1] previous_line = pascal(n-1) for i in range(len(previous_line)-1): line.append(previous_line[i] + previous_line[i+1]) line += [1] return line print(pascal(6))Alternativ können wir eine Lösung mit List Comprehension schreiben:
def pascal(n): if n == 1: return [1] else: p_line = pascal(n-1) line = [ p_line[i]+p_line[i+1] for i in range(len(p_line)-1)] line.insert(0,1) line.append(1) return line print(pascal(6))