# invisible
import numpy as np
np.core.arrayprint._line_width = 65
import matplotlib as mpl
mpl.rcParams['figure.dpi'] = 300

NumPy ist ein Akronym für "Numerisches Python" (englisch: "Numeric Python" oder "Numerical Python"). Dabei handelt es sich um ein Erweiterungsmodul für Python, welches zum größten Teil in C geschrieben ist.
Dadurch wird sichergestellt, dass die kompilierten mathematischen und numerischen Funktionen und Funktionalitäten eine größtmögliche Ausführungsgeschwindigkeit garantieren.
Außerdem bereichert NumPy die Programmiersprache Python um mächtige Datenstrukturen für das effiziente Rechnen mit großen Arrays und Matrizen.
Die Implementierung zielt sogar auf extrem große ("big data") Matrizen und Arrays. Ferner bietet das Modul eine riesige Anzahl von hochwertigen mathematischen Funktionen, um mit diesen Matrizen und Arrays zu arbeiten.
SciPy (Scientific Python) wird oft im gleichen Atemzug wie NumPy genannt. SciPy erweitert die Leistungsfähigkeit von NumPy um weitere nützliche Funktionen, wie zum Beispiel Minimierung, Regression, Fouriertransformation und vielen anderen.
Sowohl NumPy als auch SciPy sind üblicherweise bei einer Standardinstallation von Python nicht installiert. NumPy sowie all die anderen erwähnten Module sind jedoch Bestandteil der Anaconda-Distribution.
Will man NumPy jedoch manuell installieren, sollte man beachten, dass es als erstes, also vor SciPy installiert wird. NumPy kann von folgender Webseite heruntergelanden werden:
(Kommentar: Das Diagramm im Bild auf der rechten Seite ist eine grafische Visualisierung einer Matrix mit 14 Reihen und 20 Spalten. Es handelt sich um ein sogenanntes Hinton-Diagramm. Die Größe eines Quadrates innerhalb dieses Diagrammes korrespondiert zu der Größe des entsprechenden Wertes in der darzustellenden Matrix. Die Farbe bestimmt dabei, ob es sich um einen positiven oder negativen Wert handelt. In unserem Beispiel: Die Farbe Rot bezeichnet die negativen Werte und die Farbe Grün bezeichnet die positiven Werte.)
NumPy basiert auf zwei früheren Python-Modulen, die mit Arrays zu tun hatten. Eines von diesen ist Numeric. Numeric ist wie NumPy ein Python-Modul für leistungsstarke numerische Berechnungen, aber es ist heute überholt. Ein anderer Vorgänger von NumPy ist Numarray, bei dem es sich um eine vollständige Überarbeitung von Numeric handelt, aber auch dieses Modul ist heute veraltet. NumPy ist die Verschmelzung dieser beiden, d.h. es ist auf dem Code von Numeric und den Funktionalitäten von Numarray aufgebaut.
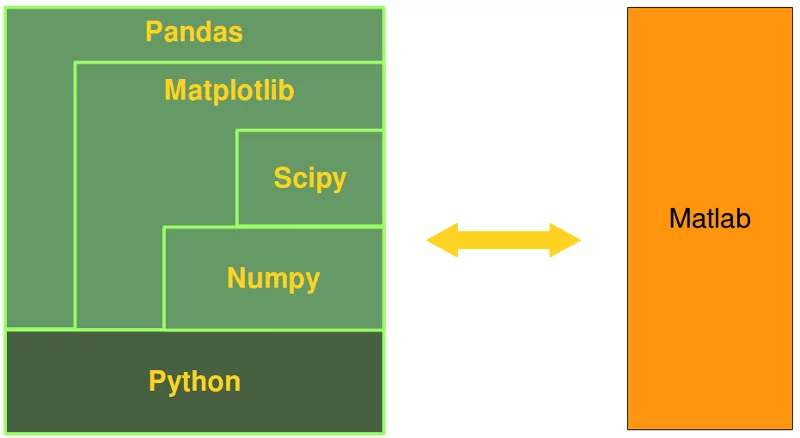
Die Python-Alternative zu MATLAB¶
Python in Kombination mit NumPy, SciPy, Matplotlib und Pandas kann prinzipiell als vollwertiger Ersatz für MATLAB genutzt werden. Bei Python und seinen Modulen handelt es sich um freie Software ("free Software" oder "open source"), frei steht hier im Sinne von "Frei"heit und nicht von "Frei"bier, auch wenn Python kostenlos ist.
Obwohl für MATLAB eine riesige Anzahl von zusätzlichen Toolboxen verfügbar sind, hat Python in Verbindung mit oben erwähnten Modulen den Vorteil, dass es sich bei Python um die modernere und umfassendere Programmiersprache handelt.
SciPy fügt weitere MATLAB-ähnliche Funktionalitäten zu Python hinzu. Das Modul Matplotlib bietet die notwendigen Plot-Funktionalitäten. Das jüngste Glied dieser Modulfamilie stellt Pandas dar. Pandas ist ideal für das Arbeiten mit Tabellendaten, wie man sie aus Tabellenkalkulationsprogrammen wie beispielsweise Excel kennt.
Vergleich zwischen Kern-Python und NumPy¶
Wenn wir von Kern-Python sprechen, dann meinen wir das reine Python ohne seine speziellen Module, also in unserem Fall NumPy.
Die Vorteile von Kern-Python:
Integers und Floats sind als mächtige Klassen implementiert. So können Integer-Zahlen beinahe "unendlich" groß oder klein werden.
Listen bieten effiziente Methoden zum Einfügen, Anhängen und Löschen von Elementen.
- Dictionaries bieten einen schnellen Lookup.
Vorteile von NumPy-Datenstrukturen gegenüber Python:
- Array-basierte Berechnungen
- Effizient implementierte mehrdimensionale Arrays
- Entworfen für wissenschaftliche Berechnungen
Ein einfaches NumPy-Beispiel¶
Bevor wir NumPy benutzen können, müssen wir es importieren. Es wird importiert wie jedes andere Modul auch:
import numpy
Die obige import-Anweisung wird man aber nur sehr selten zu sehen bekommen. Üblicherweise wird NumPy in np umbenannt:
import numpy as np
In unserem ersten einfachen NumPy-Beispiel geht es um Temperaturen. Wir definieren eine Liste mit Temperaturwerten in Celsius:
cvalues = [20.1, 20.8, 21.9, 22.5, 22.7,
21.8, 21.3, 20.9, 20.1]
Aus unserer Liste cvalues erzeugen wir nun ein eindimensionales NumPy-Array:
C = np.array(cvalues)
print(C, type(C))
Nehmen wir nun an, dass wir die Werte in Grad Fahrenheit benötigen.
Dies kann sehr einfach mit einem NumPy-Array bewerkstelligt werden. Die Lösung unseres Problems besteht in einfachen skalaren Operationen:
print(C * 9 / 5 + 32)
Das Array C selbst wurde dabei jedoch nicht verändert:
print(C)
Verglichen zu diesem Vorgehen stellt sich die Python-Lösung, die die Liste mit Hilfe einer Listen-Abstraktion website in eine Liste mit Fahrenheit-Temperaturen wandelt, als umständlich dar!
fvalues = [ x*9/5 + 32 for x in cvalues]
print(fvalues)
Wir haben bisher C als ein Array bezeichnet. Die interne Typbezeichnung lautet jedoch ndarray oder noch genauer "C ist eine Instanz der Klasse numpy.ndarray":
type(C)
Im Folgenden werden wir die Begriffe "Array" und "ndarray" meistens synonym verwenden.
Grafische Darstellung der Werte¶
Obwohl wir das Modul Matplotlib erst später im Detail besprechen werden, wollen wir zeigen, wie wir mit diesem Modul die obigen Temperaturwerte ausgeben können. Dazu benutzen wir das Paket pyplot aus matplotlib. Wenn man mit dem Jupyter-Notebook arbeitet, empfiehlt es sich, die folgende Codezeile zu verwenden, damit der Plot innerhalb des Notebooks erscheint und nicht in einem separat erscheinenden Fenster dargestellt wird:
%matplotlib inline
Sollen die Plots in einem Notebook jedoch in externen Fenstern auftauchen, schreibt man obige Zeile ohne "inline", also nur "%matplotlib".
Der Code zum Erzeugen eines Plots für unsere Werte sieht wie folgt aus:
import matplotlib.pyplot as plt
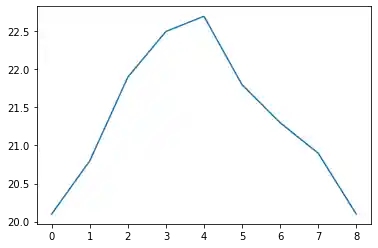
plt.plot(C)
plt.show()
Die Funktion plot benutzt das Array C als Werte für die Ordinate, also die Y-Achse. Als Werte für die Abszisse wurden die Indizes des Arrays C genommen.
Speicherbedarf¶
Die wesentlichen Vorteile von NumPy-Arrays sollten ein kleinerer Speicherverbrauch und ein besseres Laufzeitverhalten sein. Wir wollen uns den Speicherverbrauch von NumPy-Arrays in diesem Kapitel unseres Tutorials anschauen und ihn mit dem Speicherverbrauch von Python-Listen vergleichen.
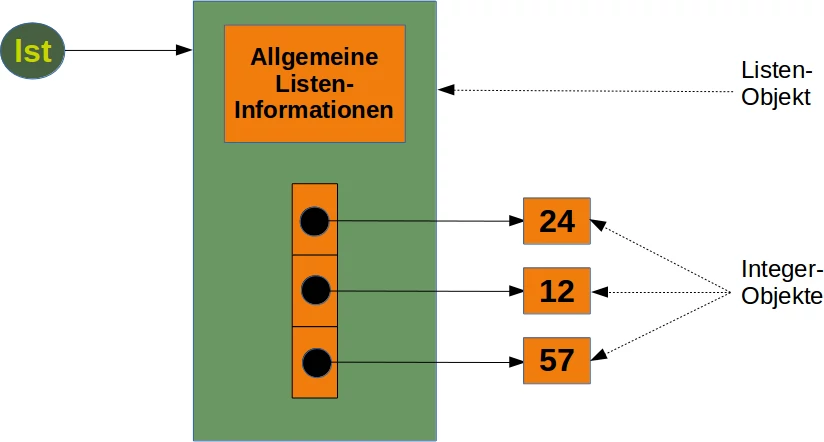
Um den Speicherverbrauch der Liste aus dem vorigen Bild zu berechnen, werden wir die Funktion getsizeof aus dem Modul sys benutzen:
from sys import getsizeof as size
lst = [24, 12, 57]
size_of_list_object = size(lst) # only green box
size_of_elements = len(lst) * size(lst[0]) # 24, 12, 57
total_list_size = size_of_list_object + size_of_elements
print("Größe ohne Größe der Elemente: ", size_of_list_object)
print("Größe aller Elemente: ", size_of_elements)
print("Gesamtgröße der Liste: ", total_list_size)
Der Speicherbedarf einer Python-Liste besteht aus der Größe der allgemeinen Listeninformation, dem Speicherbedarf für die Referenzen auf die Listenelemente und der Größe aller Elemente der Liste. Wenn wir sys.getsizeof auf eine Liste anwenden, erhalten wir nur den Speicherbedarf der reinen Liste ohne die Größe der Listenelemente. Im obigen Beispiel sind wir davon ausgegangen, dass alle Integer-Elemente unserer Liste die gleiche Größe haben. Dies stimmt natürlich nicht im allgemeinen Fall, da Integers bei steigender Größe auch einen größeren Speicherbedarf haben.
Wir wollen nun prüfen, wie sich der Speicherverbrauch ändert, wenn wir weitere Integer-Elemente zu der Liste hinzufügen. Außerdem schauen wir uns den Speicherverbrauch einer leeren Liste an:
lst = [24, 12, 57, 42]
size_of_list_object = size(lst)
size_of_elements = len(lst) * size(lst[0]) # 24, 12, 57, 42
total_list_size = size_of_list_object + size_of_elements
print("Größe ohne Größe der Elemente: ", size_of_list_object)
print("Größe aller Elemente: ", size_of_elements)
print("Gesamtgröße der Liste: ", total_list_size)
lst = []
print("Speicherbedarf einer leeren Liste: ", size(lst))
Aus den Ausgaben des vorigen Codes können wir folgern, dass wir für jedes Integer-Element 8 Bytes für die Referenz benötigen. Ein Integer-Objekt selbst benötigt in unserem Fall 28 Bytes. Die Größe der Liste "lst" ohne den Speicherbedarf für die Elemente selbst kann also in unserem Fall wie folgt berechnet werden:
64 + 8 * len(lst)
Um den kompletten Speicherbedarf einer Integer-Liste auszurechnen, müssen wir noch den Speicherbedarf aller Integer hinzuaddieren.
Nun werden wir den Speicherbedarf eines NumPy-Arrays berechnen. Zu diesem Zweck schauen wir uns zunächst die Implementierung im folgenden Bild an:

Wir erzeugen nun das Array aus dem vorigen Bild und berechnen seinen Speicherbedarf:
a = np.array([24, 12, 57])
print(size(a))
Den Speicherbedarf für die allgemeine Array-Information können wir berechnen, indem wir ein leeres Array erzeugen:
e = np.array([])
print(size(e))
Wir können sehen, dass die Differenz zwischen dem leeren Array "e" und dem Array "a", bestehend aus 3 Integern, 24 Bytes beträgt. Dies bedeutet dass sich der Speicherbedarf für ein beliebiges Integer-Array "n" wir folgt ergibt:
96 + n * 8 Bytes
Im Vergleich dazu berechnet sich der Speicherbedarf einer Integer-Liste, wie wir gesehen haben, als:
64 + 8 len(lst) + len(lst) * 28
Dies ist eine untere Schranke, da Python-Integers größer als 28 Bytes werden können!
Wenn wir ein NumPy-Array definieren, wählt NumPy automatisch eine feste Integer-Größe, in unserem Fall "int64".
Diese Größe können wir auch bei der Definition eines Arrays festlegen. Damit ändert sich natürlich auch der Gesamtspeicherbedarf des Arrays:
a = np.array([24, 12, 57], np.int8)
print(size(a) - 96)
a = np.array([24, 12, 57], np.int16)
print(size(a) - 96)
a = np.array([24, 12, 57], np.int32)
print(size(a) - 96)
a = np.array([24, 12, 57], np.int64)
print(size(a) - 96)
Zeitvergleich zwischen Python-Listen und NumPy-Arrays¶
Einer der Hauptvorteile von NumPy ist sein Zeitvorteil gegenüber Standardpython. Im Folgenden definieren wir zwei Funktionen. Die erste pure_python_version erzeugt zwei Python-Listen mittels range, während die zweite zwei NumPy-Arrays mittels der NumPy-Funktion arange erzeugt. In beiden Funktionen addieren wir die Elemente komponentenweise:
import numpy as np
import time
size_of_vec = 1000
def pure_python_version():
t1 = time.time()
X = range(size_of_vec)
Y = range(size_of_vec)
Z = [X[i] + Y[i] for i in range(len(X))]
return time.time() - t1
def numpy_version():
t1 = time.time()
X = np.arange(size_of_vec)
Y = np.arange(size_of_vec)
Z = X + Y
return time.time() - t1
Wir rufen diese Funktionen auf und können den Zeitvorteil sehen:
t1 = pure_python_version()
t2 = numpy_version()
print(t1, t2)
print("NumPy is in this example " + str(t1/t2) + " faster!")
Die Zeitmessung gestaltet sich einfacher und vor allen Dingen besser, wenn wir dazu das Modul timeit verwenden. In dem folgenden Skript werden wir die Timer-Klasse nutzen.
Dem Konstruktor eines Timer-Objektes können zwei Anweisungen übergeben werden: eine, die gemessen werden soll, und eine, die als Setup fungiert. Beide Anweisungen sind auf 'pass' per Default gesetzt. Ansonsten kann noch eine Timer-Funktion übergeben werden.
Ein Timer-Objekt hat eine timeit-Methode. Das Argument der timeit-Methode ist die Anzahl der Schleifendurchläufe, die der Code wiederholt werden soll.
timeit(number=1000000)
timeit liefert als Ergebnis die benötigte Zeit für number-Durchläufe.
import numpy as np
from timeit import Timer
size_of_vec = 1000
def pure_python_version():
X = range(size_of_vec)
Y = range(size_of_vec)
Z = [X[i] + Y[i] for i in range(len(X))]
def numpy_version():
X = np.arange(size_of_vec)
Y = np.arange(size_of_vec)
Z = X + Y
timer_obj1 = Timer("pure_python_version()",
"from __main__ import pure_python_version")
timer_obj2 = Timer("numpy_version()",
"from __main__ import numpy_version")
print(timer_obj1.timeit(10))
print(timer_obj2.timeit(10))
Die repeat-Method ist eine vereinfachte Möglichkeit, die Methode timeit mehrmals aufzurufen und eine Liste der Ergebnisse zu erhalten:
print(timer_obj1.repeat(repeat=3, number=10))
print(timer_obj2.repeat(repeat=3, number=10))

 Buch kaufen
Buch kaufen
 Buch kaufen
Buch kaufen
 Buch kaufen
Buch kaufen