Einführung in die Text-Klassifikation

Prisma as a symbol of Text classification Die Klassifikation und Kategorisierung von Dokumenten ist ein Thema der Informationswissenschaft. E ine Wissenschaft, die sich mit der Untersuchung von Informationen und Wissen beschäftigt. Dabei geht es um die Auswertung, die Selektion, das Erschließen, das Suchen und Finden, sowie das Bereitstellen und Verwerten von Informationen. Wenn es um Dokumente geht, die sich Klassen oder Kategorien zuordnen lassen, kann man sich der automatischen Dokumentenklassifikation bedienen.

Dies mag ziemlich abstrakt klingen, aber heutzutage gibt es viele Situationen, in denen Firmen die automatische Klassifikation bzw. Kategorisierung von Dokumenten benötigen. Man denke nur beispielsweise an eine große Firma, die jeden Tag Berge von Eingangspost zu bewältigen hat, sowohl in elektronischer als auch in papiergebundener Form. Üblicherweise hat ein großer Teil dieser Eingangspost weder einen korrekten Betreff noch eine Namens- oder Abteilungsnennung, aus der eindeutig hervorgeht, wohin, also zu welcher Person oder Abteilung, das Poststück weitergeleitet werden kann. Jemand muss also diese Post lesen und muss entscheiden, um welches Anliegen es geht, also beispielsweise "Adressänderung", "Beschwerdeschreiben", "Anfrage zu einem Produkt" und so weiter. Dieser "Jemand" könnte auch ein automatisches Textklassifikationssystem sein.

Die Geschichte der automatischen Textklassifikation geht zurück bis an den Anfang der 60er Jahre. Aber erst der unglaubliche Anstieg in verfügbaren Online-Dokumenten in den letzten beiden Jahrzehnten, im Zusammenhang mit der Expansion des Internets, hat das Interesse an der automatischen Dokumentenklassifikation und Data Mining erneuert und intensiviert. Anfänglich war die Dokumentenklassifikation auf heuristische Methoden fixiert, d.h. man versuchte die Aufgaben dadurch zu lösen, dass man Expertenwissen in Regelwerke packte. Dieser Ansatz stellte sich als hochgradig ineffizient für komplexe Aufgaben heraus, so dass heutzutage der Fokus auf automatischen Lernen und der Anwendung von Clustering-Methoden liegt.

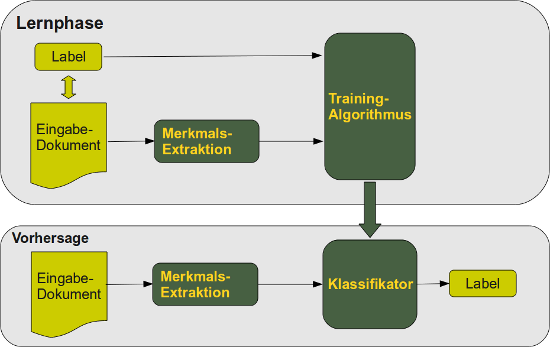
Die Aufgabe der Textklassifikation besteht darin, Dokumente in Abhängigkeit ihres semantischen Inhaltes einer oder mehreren Kategorien oder Klassen zuzuordnen. Überwachtes Lernen

Man unterscheidet eine Lernphase und eine Klassifikationsphase. Die Lernphase kann man grob in drei Arten unterteilen:
Wir werden einen Textklassifikator in Python implementieren, der auf Naive Bayes basiert ist. Naive Bayes ist der am häufigsten benutzte Textklassifikator und ist im Fokus der Forschung. Ein Naive-Bayes-Klassifikator geht von der strengen Unabhängigkeit der verwendeten Merkmale aus, d.h. das Vorhandensein oder die Abwesenheit eines bestimmten Merkmales in einer Klasse steht in keiner Beziehung zum Vorhandensein bzw. Abwesenheit von allen andern Merkmalen. Eine "naive" Annahme, die sich dennoch in der praktischen Anwendung zu hervorragenden Ergebnissen führt.

Formale Definition

C = { c1, c2, ... cm} ist eine Menge von Kategorien (Klassen)
und
D = { d1, d2, ... dn} ist eine Menge von Dokumenten.

Die Aufgabe der Textklassifikation besteht nun darin jedem Paar ( ci, dj ) ∈ C x D (mit 1 ≤ i ≤ m und 1 ≤ j ≤ n) einen Wert 0 oder 1 zuzuordnen, d.h. den Wert 0, wenn das Dokument dj nicht zur Klasse ci gehört, ansonsten 1.

Diese Abbildung wird auch als Entscheidungsmatrix bezeichnet:


d1

...

dj

...

dn

c1

a11

...

a1j

...

a1n

...

...

...

...

...

...

ci

ai1

...

aij

...

ain

...

...

...

...

...

...

cm

am1

...

amj

...

amn

Die wichtigsten Ansätze diese Aufgabe zu lösen:

Bedingte Wahrscheinlichkeit

Die bedingte Wahrscheinlichkeit (auch konditionale Wahrscheinlichkeit) bezeichnet die Wahrscheinlichkeit, dass ein Ereignis A eintritt unter der Bedingung, dass das Eintreten eines anderen Ereignisses B gegeben ist. Man notiert die bedingte Wahrscheinlichkeit als P(A|B). Der senkrechte Strich "|" zwischen A und B wird als "unter der Bedingung" gelesen.
Die Wahrscheinlichkeit, dass A und B gemeinsam in einem Zufallsexperiment auftreten wird mit

P(A ∩ B), P(AB) or P(A,B)

bezeichnet.

Die bedingte Wahrscheinlichkeit wird nun wie folgt definiert:

P(A|B) = P( A ∩ B) / P(B)

Bedingte Wahrscheinlichkeit: Beispiel

Ein medizinisches Forschungsinstitut schlägt ein Screening vor, um eine große Gruppe von Menschen auf das Vorhandensein einer bestimmten Krankheit zu untersuchen.

Ein wichtiges Gegenargument für ein solches Screening stellen die Falsch-Positiv-Ergebnisse dar:

Nehmen wir an, dass 0,1% in der Gruppe unter der Krankheit leiden und der Rest gesund ist:
P("krank") = 0,1 % = 0.01 und
P("gesund") = 99,9 % = 0.999.

Nehmen wir an, das folgende gilt für den Screening-Test:
Wenn man die Krankheit hat, ist der Test in 99 % aller Fälle positiv, wenn man aber gesund ist, ist der Test negativ in 99 % aller Fälle:
P("Test positiv" | "gesund") = 1 % und P("Test negativ" | "gesund") = 99 %.

Nehmen wir nun an, dass der Test bei einer erkrankten Person angewendet wird. Dann besteht eine Chance von 1%, dass ein falsches Negativergebnis (Falsch-Negativ) eintritt:
P("Test negativ" | "krank") = 1 % und P("Test positiv" | "krank") = 99 %


krank
 gesund
 gesamt
Testergebnis positiv
 99
 999
 1098
Testergebnis negativ
 1
 98901
 98902
Gesamt
 100
 99900
 100000


Der Tabelle können wir entnehmen, dass es also 999 Fälle von Falsch-Positiv und 1 Fall von Falsch-Negativ gibt.
Problem:
In vielen Fällen ziehen Mediziner und medizinisches Fachpersonal mangels statischem Wissen die falschen Schlüsse: Ein positives Ergebnis heißt für sie, dass ein Patient mit einer Sicherheit von 99 % erkrankt ist. In Wirklichkeit sieht es aber so aus:
Von den 1098 Fällen, in denen wir ein positives Ergebnis erhalten haben, sind nur 99 Fälle (9 %) korrekterweise Positiv, die anderen 999 Fälle (91 %) sind Falsch-Positiv.

Das bedeutet, dass nur in 9 % aller Fälle ein positives Ergebnis auch einer Erkrankung entspricht:
P("krank" | "test positive") = 99 / 1098 = 9.02 %

(Anm: Ein ähnliches Beispiel zur bedingten Wahrscheinlichkeit befindet sich auf der Webseite "Lügen mit Statistik" im Abschnitt "Mammographie und Wahrscheinlichkeit".)

Naive-Bayes-Klassifikator

Ein Naive-Bayes-Klassifikator ist ein probabilistischer Klassifikator, der nach dem englischen Mathematiker Thomas Bayes benannt ist. Er leitet sich aus dem Bayestheorem ab. Beim Naive-Bayes-Klassifikator wird jedem Objekt, in unserem Fall jedem Textdokument, eine Klasse oder Kategorie zugeordnet, zu der es mit der größten Wahrscheinlichkeit gehört.
Die zugrundeliegende Annahme beim Naive-Bayes-Klassifikator besteht darin, von einer strengen Unabhängigkeit der verwendeten Merkmale auszugehen, d.h. das Vorhandensein oder die Abwesenheit eines bestimmten Merkmales in einer Klasse steht in keiner Beziehung zum Vorhandensein bzw. Abwesenheit von allen andern Merkmalen. Diese Annahme ist mit dem Namensbestandteil "Naive" gemeint. Eine Voraussetzung, die in der praktischen Anwendung des Naive-Bayes-Konzeptes meist nicht gegeben ist, aber dennoch werden häufig mit diesem "naiven" Ansatz ausreichend gute Ergebnisse erzielt und das bei einer schnellen Berechenbarkeit durch die sich der NBK auszeichnet.

Bayestheorem

Definition unabhängiger Ereignisse:
Zwei Ereignisse E und F sind unabhängig, wenn das Auftreten von E die Wahrscheinlichkeit, dass F eintritt, nicht beeinflusst und umgekehrt:

P(E|F) = P(E) und
P(F|E) = P(F)

Bayestheorem:
P(A|B) = P(B|A)P(A) / P(B)

P(A|B) bezeichnet die bedingte Wahrscheinlichkeit für ein Ereignis A unter der Bedingung, dass B gilt. P(A|B) wird im Zusammenhang mit dem Bayestheorem häufig auch als A-posteriori-Wahrscheinlichkeit bezeichnet.
P(B) ist die A-priori-Wahrscheinlichkeit für das Ereignis B und P(A) ist die A-priori-Wahrscheinlichkeit für das Ereignis A.
(B|A) bezeichnet die bedingte Wahrscheinlichkeit für ein Ereignis B unter der Bedingung, dass A gilt, auch bezeichnet als likelyhood.

Ein Vorteil des Naive-Bayes-Klassifikators besteht darin, dass er nur eine kleine Trainingsmenge benötigt, um die zur Klassifikation notwendigen Parameter einzustellen.

Formale Herleitung der Naive-Bayes-Klassifikation:

Formel der Textklassifikation Sei C = { c1, c2, ... cm} eine Menge von Klassen oder Kategorien und D = { d1, d2, ... dn} eine Menge von Dokumenten.
Jedes Dokument ist mit einer Klasse etikettiert (labelled).
Die Menge D von Dokumenten wird benötigt um den Klassifikator zu trainieren.
Die Klassifikation besteht darin, die wahrscheinlichste Klasse für ein unbekanntes Dokument auzuwählen.

Wir bezeichnen die Anzahl der Vorkommen eines Wortes wt in einem Dokument di mit Nit.
NtC bezeichnet die Anzahl der Vorkommen eines Wortes wt in allen Dokumenten einer gegebenen Klasse C.
P(di|cj) ist 1, falls di mit cj etikettiert ist, ansonsten 0.

Die Wahrscheinlichkeit für ein Wort wt unter der Bedingung, dass die Klasse cj gegeben wird wie folgt berechnet:

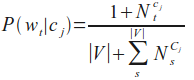
Wahrscheinlichkeit für ein Wort bei gegebener Klasse

Die Wahrscheinlichkeit P(cj) für eine Klasse cj ist der Quotient aus der Anzahl der Dokumente der Klasse cj und der Anzahl der Dokumente aller Klassen, d.h. des Lernsets:

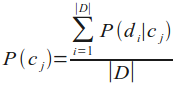
Wahrscheinlichkeit für ein gegebenes Dokument

Nun kommen wir zu der Formel, die wir zur Klassifikation eines Dokumentes benötigt, d.h. die Wahrscheinlichkeit für eine Klasse cj unter der Bedingung, dass ein Dokument di gegeben ist:

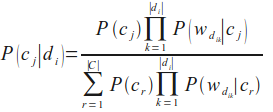
Die Klassifikationsformel: die Wahrscheinlichkeit für eine Klasse unter der Bedingung, dass ein Dokument gegeben ist.

Leider ist die vorherige Formel für P(c|di) numerisch nicht stabil, weil der Nenner wegen fortschreitenden Rundungsfehlern Null werden kann. Wir ändern dies, indem wir den Kehrwert berechnen und den Ausdruck als Summe von stabilen Quotienten berechnen:

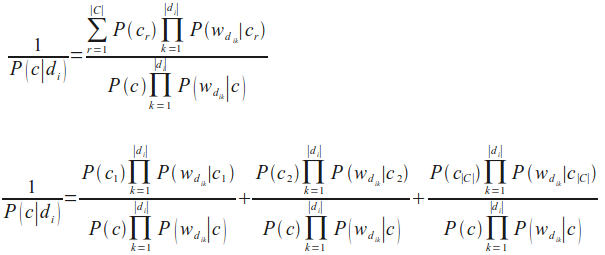
Die Klassifikationsformel in einer numerisch stabilen Form.

Die vorherige Formel können wir durch weitere Umformungen in unsere finale Naive-Bayes-Klassifikationsformel überführen, die wir im nächsten Kapitel in Python implementieren werden:

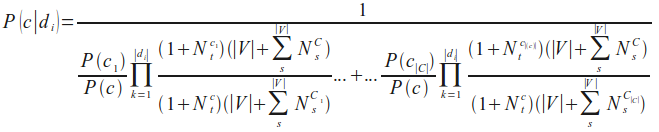
Die finale Klassifikationsformel in einer numerisch stabilen Form.

Weiterführende Literatur

Es gibt eine Vielzahl von Artikel zur Textklassifikation. Wir wollen nur einige nennen, die wir für unsere Arbeit besonders nützlich fanden: