Lambda, filter, reduce and map
Wenn Guido van Rossum, der Autor der Programmiersprache Python, seinen Willen bekommen hätte, hätte dieses Kapitel in unserem Tutorial gefehlt. In seinem Artikel vom Mai 2005 "All Things Pythonic: Das Schicksal von reduce () in Python 3000" gibt er seine Gründe dafür an Löschen von Lambda, Map (), Filter () und Reduzieren (). Er erwartete Widerstand von den Lisp und dem Schema "Leute". Was er nicht erwartet hatte, war die Starrheit dieser Opposition. Genug, dass Guido van Rossum kaum ein Jahr später schrieb: "Nach so vielen Versuchen, eine Alternative für Lambda zu finden, sollten wir uns vielleicht geschlagen geben. Ich hatte nicht die Zeit, die letzten Runden zu verfolgen, aber ich schlage vor, dass wir Behalte Lambda, um nicht länger das Talent und die Zeit aller für eine unmögliche Suche zu verschwenden. " Wir können das Ergebnis sehen: Lambda, Map () und Filter () sind immer noch Teil von Python. Nur reduce () musste gehen; es wurde in die Modul-Funktools verschoben.
Seine Argumentation, sie fallen zu lassen, lautet wie folgt:
- Es gibt eine ebenso leistungsfähige Alternative zu Lambda, Filtern, Zuordnen und Reduzieren, d. H. Listenverständnis
- List Comprehension (ist offensichtlicher und leichter zu verstehen
- Sowohl Listenverständnis als auch "Filtern, Zuordnen, Reduzieren und Lambda" verstoßen gegen das Python-Motto "Es sollte einen offensichtlichen Weg geben, ein Problem zu lösen".
Einige mögen es, andere hassen es und viele haben Angst vor dem Lambda-Betreiber. Der Lambda-Operator oder die Lambda-Funktion ist eine Möglichkeit, kleine anonyme Funktionen zu erstellen, d. H. Funktionen ohne Namen. Diese Funktionen sind Wegwerffunktionen, d. H. Sie werden nur dort benötigt, wo sie erstellt wurden. Lambda-Funktionen werden hauptsächlich in Kombination mit den Funktionen filter (), map () und reduce () verwendet. Die Lambda-Funktion wurde Python aufgrund der Nachfrage von Lisp-Programmierern hinzugefügt.
Die allgemeine Syntax einer Lambda-Funktion ist recht einfach:
lambda argument_list: Ausdruck
Die Argumentliste besteht aus einer durch Kommas getrennten Liste von Argumenten, und der Ausdruck ist ein arithmetischer Ausdruck, der diese Argumente verwendet. Sie können die Funktion einer Variablen zuweisen, um ihr einen Namen zu geben.
Das folgende Beispiel einer Lambda-Funktion gibt die Summe ihrer beiden Argumente zurück:
summe = lambda x, y : x + y
summe(3,4)
Das obige Beispiel könnte wie ein Spielzeug für einen Mathematiker aussehen. Ein Formalismus, der ein leicht verständliches Thema in ein abstraktes, schwerer zu fassendes Formalismus verwandelt. Vor allem hätten wir den gleichen Effekt erzielen können, wenn wir nur die folgende herkömmliche Funktionsdefinition verwendet hätten:
def summe(x,y):
return x + y
summe(3,4)
Wir können Ihnen versichern, dass die Vorteile dieses Ansatzes offensichtlich werden, wenn Sie gelernt haben, die Funktion map () zu verwenden.
Die Funktion map ()
Wie bereits erwähnt, zeigt sich der Vorteil des Lambda-Operators in Kombination mit der Funktion map (). map () ist eine Funktion, die zwei Argumente akzeptiert:
r = map (func, seq)
Das erste Argument func ist der Name einer Funktion und das zweite eine Sequenz (z. B. eine Liste) seq. map () wendet die Funktion func auf alle Elemente der Sequenz seq an. Vor Python3 gab map () eine Liste zurück, wobei jedes Element der Ergebnisliste das Ergebnis der Funktion func war, die auf das entsprechende Element der Liste oder das Tupel "seq" angewendet wurde. Mit Python 3 gibt map () einen Iterator zurück.
Das folgende Beispiel zeigt die Arbeitsweise von map ():
def fahrenheit(T):
return ((float(9)/5)*T + 32)
def celsius(T):
return (float(5)/9)*(T-32)
temperaturen = (36.5, 37, 37.5, 38, 39)
F = map(fahrenheit, temperaturen)
C = map(celsius, F)
temperaturen_in_Fahrenheit = list(map(fahrenheit, temperaturen))
temperaturen_in_Celsius = list(map(celsius, temperaturen_in_Fahrenheit))
print(temperaturen_in_Fahrenheit)
print(temperaturen_in_Celsius)
Im obigen Beispiel haben wir kein Lambda verwendet. Mit Lambda hätten wir die Funktionen fahrenheit () und celsius () nicht definieren und benennen müssen. Sie können dies in der folgenden interaktiven Sitzung sehen:
C = [39.2, 36.5, 37.3, 38, 37.8]
F = list(map(lambda x: (float(9)/5)*x + 32, C))
print(F)
C = list(map(lambda x: (float(5)/9)*(x-32), F))
print(C)
map () kann auf mehrere Listen angewendet werden. Die Listen müssen nicht gleich lang sein. map () wendet seine Lambda-Funktion auf die Elemente der Argumentlisten an, d. h. es gilt zuerst für die Elemente mit dem 0. Index und dann für die Elemente mit dem 1. Index, bis der n-te Index erreicht ist:
a = [1, 2, 3, 4]
b = [17, 12, 11, 10]
c = [-1, -4, 5, 9]
list(map(lambda x, y, z : x+y+z, a, b, c))
list(map(lambda x, y : x+y, a, b))
list(map(lambda x, y, z : 2.5*x + 2*y - z, a, b, c))
Wenn eine Liste weniger Elemente als die anderen enthält, wird die Karte angehalten, wenn die kürzeste Liste verwendet wurde:
a = [1, 2, 3]
b = [17, 12, 11, 10]
c = [-1, -4, 5, 9]
list(map(lambda x, y, z : 2.5*x + 2*y - z, a, b, c))
Wir können im obigen Beispiel sehen, dass der Parameter x seine Werte aus der Liste a erhält, während y seine Werte aus b und z aus der Liste c erhält.
Zuordnen einer Liste von Funktionen
Die Kartenfunktion des vorherigen Kapitels wurde verwendet, um eine Funktion auf eine oder mehrere Iterables anzuwenden. Wir werden nun eine Funktion schreiben, die eine Reihe von Funktionen anwendet, die iterativ sein können, z. B. eine Liste oder ein Tupel, beispielsweise auf ein Python-Objekt.
from math import sin, cos, tan, pi
def map_funktionen(x, funktionen):
""" Ordnen Sie dem Objekt x eine Iterable von Funktionen zu. """
res = []
for func in funktionen:
res.append(func(x))
return res
familie_von_funktionen = (sin, cos, tan)
print(map_funktionen(pi, familie_von_funktionen))
Die zuvor definierte Funktion map_functions kann mit der Listenverständnis-Technik vereinfacht werden, die wir im Kapitel List Comprehensions behandeln werden:
def map_functions(x, functions):
return [ func(x) for func in functions ]
Filtern
Die Funktion
Filter (Funktion, Reihenfolge)
bietet eine elegante Möglichkeit, alle Elemente einer Sequenz "Sequenz" herauszufiltern, für die die Funktionsfunktion True zurückgibt. d.h. ein Element wird durch das Iteratorergebnis des Filters (Funktion, Sequenz) erzeugt, wenn das Element in der Sequenz "Sequenz" enthalten ist und wenn die Funktion (Element) True zurückgibt.
Mit anderen Worten: Der Funktionsfilter (f, l) benötigt eine Funktion f als erstes Argument. f muss einen booleschen Wert zurückgeben, d. h. entweder True oder False. Diese Funktion wird auf jedes Element der Liste l angewendet. Nur wenn f True zurückgibt, wird das Element vom Iterator erzeugt. Dies ist der Rückgabewert des Filters (Funktion, Sequenz).
Im folgenden Beispiel filtern wir zuerst die ungeraden und dann die geraden Elemente der Folge der ersten 11 Fibonacci-Zahlen heraus:
fibonacci = [0,1,1,2,3,5,8,13,21,34,55]
ungerade_zahlen = list(filter(lambda x: x % 2, fibonacci))
print(ungerade_zahlen)
gerade_zahlen = list(filter(lambda x: x % 2 == 0, fibonacci))
print(gerade_zahlen)
gerade_zahlen = list(filter(lambda x: x % 2 -1, fibonacci))
print(gerade_zahlen)
Eine Liste reduzieren
Wie wir in der Einleitung dieses Kapitels unseres Tutorials erwähnt haben. reduce () wurde bei der Migration auf Python 3 aus dem Kern von Python entfernt. Guido van Rossum hasst reduce (), wie wir aus seiner Aussage in einem Posting vom 10. März 2005 auf artima.com erfahren können:
"Also jetzt reduziere (). Dies ist eigentlich die, die ich immer am meisten gehasst habe, denn abgesehen von ein paar Beispielen mit + oder *, fast jedes Mal, wenn ich einen reduzierten () Aufruf mit einem nicht trivialen Funktionsargument sehe, ich Ich muss Stift und Papier greifen, um darzustellen, was tatsächlich in diese Funktion eingespeist wird, bevor ich verstehe, was reduce () tun soll. Meiner Meinung nach ist die Anwendbarkeit von reduce () also weitgehend auf assoziative Operatoren beschränkt In anderen Fällen ist es besser, die Akkumulationsschleife explizit auszuschreiben. "
Die Funktion
reduzieren (func, seq)
wendet kontinuierlich die Funktion func () auf die Sequenz seq an. Es wird ein einzelner Wert zurückgegeben.
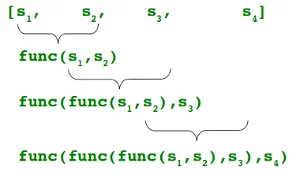
Wenn seq = [s1, s2, s3, ..., sn], funktioniert der Aufruf von reduce (func, seq) folgendermaßen:
Zuerst werden die ersten beiden Elemente von seq auf func angewendet, d. H. Func (s1, s2). Die Liste, auf der reduce () funktioniert, sieht jetzt folgendermaßen aus: [func (s1, s2), s3, ..., sn]
Im nächsten Schritt wird func auf das vorherige Ergebnis und das dritte Element der Liste angewendet, d. H. Func (func (s1, s2), s3).
Die Liste sieht jetzt so aus: [func (func (s1, s2), s3), ..., sn]
Fahren Sie so fort, bis nur noch ein Element übrig ist, und geben Sie dieses Element als Ergebnis von reduce () zurück.
Wenn n gleich 4 ist, kann die vorherige Erklärung folgendermaßen dargestellt werden:
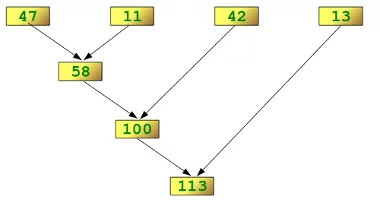
Wir wollen diese Arbeitsweise von reduce() anhand eines einfachen Beispiels veranschaulichen. Wir müssen functools importieren, um reduzieren zu können:
import functools
functools.reduce(lambda x,y: x+y, [47,11,42,13])
Das folgende Diagramm zeigt die Zwischenschritte der Berechnung:
from functools import reduce
f = lambda a,b: a if (a > b) else b
reduce(f, [47,11,42,102,13])
Berechnung der Summe der Zahlen von 1 bis 100:
from functools import reduce
reduce(lambda x, y: x+y, range(1,101))
Es ist sehr einfach, das vorherige Beispiel zu ändern, um das Produkt (die Fakultät) von 1 in eine Zahl zu berechnen, aber wählen Sie nicht 100. Wir müssen nur den Operator "+" in "*" umwandeln:
reduce(lambda x, y: x*y, range(1,49))
Wenn Sie in der Lotterie interessiert sind, sind hier die Chancen, eine 6 von 49 Ziehungen zu gewinnen:
reduce(lambda x, y: x*y, range(44,50))/reduce(lambda x, y: x*y, range(1,7))
Übungen
1) Stellen Sie sich eine Buchhaltungsroutine vor, die in einem Buchladen verwendet wird. Es funktioniert auf einer Liste mit Unterlisten, die folgendermaßen aussehen:
Order Number Book Title and Author Quantity Price per Item
34587 Learning Python, Mark Lutz 4 40.95
98762 Programming Python, Mark Lutz 5 56.80
77226 Head First Python, Paul Barry 3 32.95
88112 Einführung in Python3, Bernd Klein 3 24.99
Schreiben Sie ein Python-Programm, das eine Liste mit 2 Tupeln zurückgibt. Jedes Tupel besteht aus einer Bestellnummer und dem Produkt aus dem Preis pro Artikel und der Menge. Das Produkt sollte um 10, - € erhöht werden, wenn der Wert der Bestellung kleiner als 100,00 € ist. Schreiben Sie ein Python-Programm mit Lambda und Map.
2) Dieselbe Buchhandlung, aber diesmal arbeiten wir an einer anderen Liste. Die Unterlisten unserer Listen sehen folgendermaßen aus: [Bestellnummer, (Artikelnummer, Menge, Preis pro Einheit), ... (Artikelnummer, Menge, Preis pro Einheit)] Schreiben Sie ein Programm, das eine Liste von zwei Tupeln mit (Bestellnummer, Gesamtbestellmenge) zurückgibt.
Solutions to the Exercises
bestellungen = [ ["34587", "Learning Python, Mark Lutz", 4, 40.95],
["98762", "Programming Python, Mark Lutz", 5, 56.80],
["77226", "Head First Python, Paul Barry", 3,32.95],
["88112", "Einführung in Python3, Bernd Klein", 3, 24.99]]
min_bestellung= 100
rechnung_summen = list(map(lambda x: x if x[1] >= min_bestellung else (x[0], x[1] + 10),
map(lambda x: (x[0],x[2] * x[3]), bestellungen)))
print(rechnung_summen)
from functools import reduce
bestellungen = [ [1, ("5464", 4, 9.99), ("8274",18,12.99), ("9744", 9, 44.95)],
[2, ("5464", 9, 9.99), ("9744", 9, 44.95)],
[3, ("5464", 9, 9.99), ("88112", 11, 24.99)],
[4, ("8732", 7, 11.99), ("7733",11,18.99), ("88112", 5, 39.95)] ]
min_bestellung = 100
rechnung_summen = list(map(lambda x: [x[0]] + list(map(lambda y: y[1]*y[2], x[1:])), bestellungen))
rechnung_summen = list(map(lambda x: [x[0]] + [reduce(lambda a,b: a + b, x[1:])], rechnung_summen))
rechnung_summen = list(map(lambda x: x if x[1] >= min_bestellung else (x[0], x[1] + 10), rechnung_summen))
print(rechnung_summen)


 Informationen zum Buch
Informationen zum Buch

