Recursive Functions
Definition

"Rekursion hat etwas mit Unendlichkeit zu tun. Ich weiß, dass Rekursion etwas mit Unendlichkeit zu tun hat. Ich glaube, ich weiß, dass Rekursion etwas mit Unendlichkeit zu tun hat. Er ist sich sicher, dass ich weiß, dass Rekursion etwas mit Unendlichkeit zu tun hat. Wir bezweifeln, dass er sicher ist, dass ich weiß ..." Wir glauben, dass wir Sie jetzt davon überzeugt haben, dass wir mit diesem Beispiel einer Rekursion aus der natürlichen Sprache für immer weitermachen können. Rekursion ist nicht nur ein grundlegendes Merkmal der natürlichen Sprache, sondern auch der kognitiven Fähigkeiten des Menschen. Unsere Denkweise basiert auf rekursiven Denkprozessen. Selbst mit einer sehr einfachen Grammatikregel wie "Ein englischer Satz enthält ein Subjekt und ein Prädikat und ein Prädikat enthält ein Verb, ein Objekt und eine Ergänzung" können wir die unendlichen Möglichkeiten der natürlichen Sprache demonstrieren. Der Kognitionswissenschaftler und Linguist Stephen Pinker formuliert es so: "Mit ein paar tausend Substantiven, die den Platzhalter für das Subjekt füllen können, und ein paar tausend Verben, die den Platzhalter für das Prädikat füllen können, hat man bereits mehrere Millionen Möglichkeiten, einen Satz zu öffnen. Die möglichen Kombinationen multiplizieren sich schnell zu unvorstellbar großen Zahlen. In der Tat ist das Repertoire an Sätzen theoretisch unendlich, weil die Sprachregeln einen Trick verwenden, der als Rekursion bezeichnet wird. Eine rekursive Regel erlaubt es einer Phrase, ein Beispiel für sich selbst zu enthalten, wie in "Sie glaubt, dass er das denkt sie denken, dass er es weiß" und so weiter, ad infinitum. Und wenn die Anzahl der Sätze unendlich ist, ist auch die Anzahl der möglichen Gedanken und Absichten unendlich, weil praktisch jeder Satz einen anderen Gedanken oder eine andere Absicht ausdrückt. "1
Wir müssen unsere kurze Exkursion zur Verwendung der Rekursion in natürlicher Sprache beenden, um zur Rekursion in Informatik und Programmen und schließlich zur Rekursion in der Programmiersprache Python zurückzukehren.
Das Adjektiv "rekursiv" stammt vom lateinischen Verb "recurrere" ab, was "zurücklaufen" bedeutet. Und dies ist, was eine rekursive Definition oder eine rekursive Funktion tut: Sie "läuft zurück" oder kehrt zu sich selbst zurück. Die meisten Leute, diesich mit Mathematik oder Informatik beschäftigt haben oder ein Buch über Programmierung gelesen haben, werden auf die Fakultät gestoßen sein, die in mathematischen Begriffen definiert ist als
n! = n * (n-1)!, wenn n> 1 und 0! = 1
Es wird wegen seiner Einfach- und Klarheit oft als erstes Beispiel für eine Rekursion verwendet.
Definition der Rekursion
Rekursion ist eine Methode zum Programmieren oder Codieren eines Problems, bei der eine Funktion ein- oder mehrmals in ihrem Funktionskörper aufgerufen wird. Normalerweise wird der Rückgabewert dieses Funktionsaufrufs zurückgegeben. Wenn eine Funktionsdefinition die Rekursionsbedingung erfüllt, nennen wir diese Funktion eine rekursive Funktion.
Abbruchbedingung: Eine rekursive Funktion muss eine wichtige Bedingung erfüllen, damit man sie in einem Programm verwenden kann: Sie muss terminieren. Eine rekursive Funktion wird beendet, wenn bei jedem rekursiven Aufruf die Lösung des Problems verkleinert wird und sich einem Basisfall "nähert". Ein Basisfall ist ein Fall, in dem das Problem ohne weitere Rekursion gelöst werden kann. Eine Rekursion kann in einer Endlosschleife enden, wenn der Basisfall in den Aufrufen nicht erreicht wird.
Beispiel:
4! = 4 * 3! 3! = 3 * 2! 2! = 2 * 1! 1! = 1
Das Ersetzen der berechneten Werte ergibt den folgenden Ausdruck
4! = 4 * 3 * 2 * 1Mit anderen Worten, Rekursion in der Informatik ist eine Methode, bei der die Lösung eines Problems auf der Lösung kleinerer Instanzen desselben Problems basiert.
Rekursive Funktionen in Python
Nun kommen wir dazu, die Fakultät in Python zu implementieren. Es ist so einfach und elegant wie die mathematische Definition.
def Fakultät(n):
if n == 1:
return 1
else:
return n * Fakultät(n-1)
print(Fakultät(4))
Wir können die Funktionsweise der Funktion verfolgen, indem wir der vorherigen Funktionsdefinition zwei print()-Funktionen hinzufügen:
def Fakultät(n):
print(f"Fakultät wurde mit {n} aufgerufen")
if n == 1:
return 1
else:
res = n * Fakultät(n-1)
print("Zwischenergebnis für ", n, " *Fakultät (" , n-1, "): ", res)
return res
print(Fakultät(5))
Schauen wir uns eine iterative Version der Fakultätsfunktion an.
def iterative_Fakultät(n):
Ergebnis = 1
for i in range(2, n+1):
Ergebnis *= i
return Ergebnis
for i in range(5):
print(i, iterative_Fakultät(i))
Es ist üblich, die Fakultätsfunktion für 0 als Argument zu erweitern. Es ist sinnvoll, "0!" als "1" zu definieren, da es genau eine Permutation von Nullobjekten gibt, d.h. wenn nichts permutieren soll, bleibt "Alles" an Ort und Stelle.
Für die mathematisch Interessierten: Zur Berechnung der k-Kombinationen von n Elementen gilt die Formel: $$\binom{n}{k} = \frac{n!}{(n-k)! \cdot k!}$$ Ist k gleich n, erhält man den Ausdruck $(n - n)!$ also 0!. Hierbei muss $0!$ auch als 1 definiert sein.
Um dies zu implementieren, müssen wir lediglich die Bedingung der if-Anweisung ändern:
def Fakultät(n):
if n == 0:
return 1
else:
return n * Fakultät(n-1)
Fibonacci-Zahlen
Unsere Abhandlung über die Rekursion führt uns nun zu einem weiteren interessanten Fall der Rekursion.
Was haben Sonnenblumen, der Goldene Schnitt, Tannenzapfen, der Da Vinci-Code, das Lied "Lateralus" von Tool und die Grafik auf der rechten Seite gemeinsam? Richtig, die Fibonacci-Zahlen. Die Fibonacci-Zahlen führen wir nicht ein, um ein weiteres Beispiel für eine rekursive Funktion zu haben. Vielmehr wollen wir mit einer rekursiven Funktion für diese Zahlenfolge auf ein interessantes Problem der Rekursion zu sprechen kommen. Der Versuch, eine rekursive Funktion für diese Zahlenfolge zu schreiben, kann nämlich zu einem ineffizienten Programm führen. In der Tat so ineffizient, dass es in der Praxis nicht brauchbar sein wird. Wir führen die Fibonacci-Zahlen ein, um die Fallstricke der Rekursion zu zeigen.
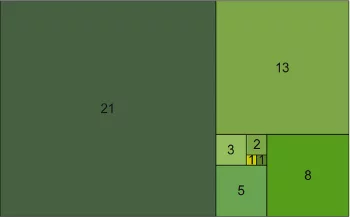
Die folgenden Zahlen stellen den Beginn der Fibonaccifolge dar:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
Schaut man diese Zahlen etwas genauer kann, kann man das Bildungsprinzip der Folge leicht erkennen. Eine Fibonacci-Zahl ist jeweils die Summe aus ihren beiden Vorgängern. Diese Gesetzmäßigkeit gilt für alle Fibonacci-Zahlen außer für die erste und die zweite, die mit 0 und 1 vorbesetzt sind:
$ F_n = F_{n-1} + F_{n-2} $
mit $F_0 = 0$ und $F_1 = 1$
Die Fibonacci-Sequenz ist nach dem Mathematiker Leonardo von Pisa benannt, der besser als Fibonacci bekannt ist. In seinem Buch "Liber Abaci" (veröffentlicht 1202) stellte er diese Folge als Übungsaufgabe vor. Seine Folge der Fibonacci-Zahlen beginnt mit $F_1 = 1$, während in der modernen Mathematik die Folge mit $F_0 = 0$ beginnt. Dies hat jedoch keine Auswirkung auf die anderen Elemente der Folge.
Die Fibonacci-Zahlen basieren auf dem von Fibonacci erdachten Populationsverhalten von Kaninchen. Sie erfüllen folgende Bedingungen:
- Ein neugeborenes Kaninchenpaar, also ein Männchen und ein Weibchen, bildet die ursprüngliche Population
- Diese Kaninchen können sich im Alter von einem Monat paaren, so dass ein Weibchen am Ende seines zweiten Monats ein weiteres Kaninchenpaar zur Welt bringen kann.
- Diese Kaninchen sind unsterblich.
- Ein Paar produziert ab dem zweiten Monat jeden Monat ein neues Paar (ein Männchen, ein Weibchen)
Wie bereits gesagt: So sah es bei Fibonacci aus. Die moderne Mathematik setzt noch eins voran: "Im Anfang gibt es keine Kaninchen". Dann nach einem Monat gibt es plötzlich ein Parr, wo immer es herkommen mag.
Die Fibonacci-Zahlen sind die Zahlen der Kaninchenpaare nach n Monaten, d.h. nach 10 Monaten haben wir $F_10$ Kaninchen.
Die Fibonacci-Zahlen sind einfach als Python-Funktion zu schreiben. Es ist mehr oder weniger eine Eins-zu-Eins-Abbildung aus der mathematischen Definition:
def fib(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
Eine iterative Lösung ist geringfügig schwerer zu schreiben, aber sollte trotzdem leicht verständlich sein, auch wenn sie nicht mehr die mathematischen Definition widerspiegelt:
def fibi(n):
alt, neu = 0, 1
if n == 0:
return 0
for i in range(n-1):
alt, neu = neu, alt + neu
return neu
Wir werden ein Modul mit dem Namen fibonacci schreiben, das sowohl die Funktion fib als auch fibi enthält. Dazu müssen Sie den folgenden Code in eine Datei mit dem Namen fibonacci0.py kopieren:
%%writefile fibonacci0.py
""" Ein Modul, das sowohl eine rekursive als auch eine iterative Implementierung
der Fibonacci-Funktion enthält. Der Zweck dieses Moduls besteht darin,
die Ineffizienz einer rein rekursiven Implementierung von Fibonacci zu zeigen! """
def fib(n):
""" rekursive Version der Fibonacci-Funktion """
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
def fibi(n):
""" iterative Version der Fibonacci-Funktion """
alt, neu = 0, 1
if n == 0:
return 0
for i in range(n-1):
alt, neu = neu, alt + neu
return neu
Vergleicht man die Laufzeiten von fib und fibi überprüfen, kann man feststellen, dass die iterative Version fibi viel schneller ist als die rekursive Version fib. Um eine Vorstellung davon zu bekommen, wie viel dies "viel schneller" sein kann, haben wir ein Skript geschrieben, das das timeit-Modul verwendet, um die Aufrufe zu messen. Dazu speichern wir die Funktionsdefinitionen für fib und fibi in einer Datei fibonacci.py, die wir in das folgende Programm (fibonacci_runit.py) importieren können:
from timeit import Timer
t1 = Timer("fib(10)","from fibonacci0 import fib")
for i in range(1, 20):
cmd = "fib(" + str(i) + ")"
t1 = Timer(cmd, "from fibonacci0 import fib")
time1 = t1.timeit(3)
cmd = "fibi(" + str(i) + ")"
t2 = Timer(cmd, "from fibonacci0 import fibi")
time2 = t2.timeit(3)
print(f"n={i:2d}, fib: {time1:8.6f}, fibi: {time2:7.6f}, time1/time2: {time1/time2:10.2f}")
time1 ist die Zeit in Sekunden, die für 3 Aufrufe von fib(n)und time2 die Zeit für fibi(n) benötigt wird .
Was ist falsch an unserer rekursiven Implementierung?
Schauen wir uns den Berechnungsbaum an, d.h. die Reihenfolge, in der die Funktionen aufgerufen werden. In den Baum steht f() statt fib().
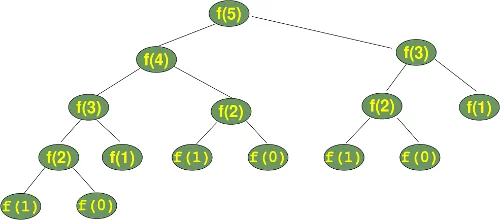
Wir können sehen, dass der Teilbaum f(2) dreimal und der Teilbaum für die Berechnung von f(3) zweimal erscheint. Wenn Sie sich vorstellen, diesen Baum für f(6) zu erweitern, werden Sie verstehen, dass f(4) zweimal, f(3) dreimal und so weiter aufgerufen wird. Dies bedeutet, dass sich unsere Rekursion nicht an zuvor berechnete Werte erinnert.
Wir können einen "Speicher" für unsere rekursive Version implementieren, indem wir ein Dictionary verwenden, um die zuvor berechneten Werte zu speichern. Wir nennen diese Version fibm:
memo = {0:0, 1:1}
def fibm(n):
if not n in memo:
memo[n] = fibm(n-1) + fibm(n-2)
return memo[n]
Wir fügen diese Funktion unserem Fibonacci-Modul hinzu:
%%writefile fibonacci.py
""" Ein Modul, das sowohl eine rekursive als auch eine iterative Implementierung der Fibonacci-Funktion enthält.
Der Zweck dieses Moduls besteht darin, die Ineffizienz einer rein rekursiven Implementierung von Fibonacci zu zeigen! """
def fib(n):
""" rekursive Version der Fibonacci-Funktion """
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
def fibi(n):
""" iterative Version der Fibonacci-Funktion """
old, new = 0, 1
if n == 0:
return 0
for i in range(n-1):
old, new = new, old + new
return new
memo = {0:0, 1:1}
def fibm(n):
""" rekursive Fibonacci-Funktion, die zuvor berechnete Werte mithilfe eines Wörterbuch-Memos gespeichert hat"""
if not n in memo:
memo[n] = fibm(n-1) + fibm(n-2)
return memo[n]
Nun können wir Zeitmessungen durchführen und die neue Funktion mit fibi vergleichen:
from timeit import Timer
from fibonacci import fib
t1 = Timer("fib(10)","from fibonacci import fib")
for i in range(1, 20):
s = "fibm(" + str(i) + ")"
t1 = Timer(s,"from fibonacci import fibm")
time1 = t1.timeit(3)
s = "fibi(" + str(i) + ")"
t2 = Timer(s,"from fibonacci import fibi")
time2 = t2.timeit(3)
print(f"n={i:2d}, fibm: {time1:8.6f}, fibi: {time2:7.6f}, time1/time2: {time1/time2:10.2f}")
Wir können sehen, dass es noch schneller als die iterative Version ist. Je größer die Argumente sind, desto größer ist natürlich der Nutzen unseres Auswendiglernens:
Wir können auch einen rekursiven Algorithmus für unsere Fibonacci-Funktion definieren, indem wir eine Klasse mit Callable-Instanzen verwenden, d.h. indem wir die spezielle Methode __call__ verwenden. Auf diese Weise können wir das Dictionary auf elegante Weise ausblenden. Wir haben einen allgemeinen Ansatz verwendet, der es erlaubt, auch Funktionen zu definieren, die der Fibonaccifolge ähnlich sind, wie beispielsweise die Lucas-Funktion:
class Fibonacci:
def __init__(self, i1=0, i2=1):
self.memo = {0:i1, 1:i2}
def __call__(self, n):
if n not in self.memo:
self.memo[n] = self.__call__(n-1) + self.__call__(n-2)
return self.memo[n]
fib = Fibonacci()
lucas = Fibonacci(2, 1)
for i in range(1, 16):
print(i, fib(i), lucas(i))
Die Lucas-Zahlen oder Lucas-Reihen sind eine ganzzahlige Folge, die nach dem Mathematiker François Édouard Anatole Lucas (1842–91) benannt ist, der sowohl diese Folge als auch die eng verwandten Fibonacci-Zahlen studierte. Die Lucas-Zahlen haben dieselbe Erstellungsregel wie die Fibonacci-Zahl, d.h. die Summe der beiden vorherigen Zahlen, aber die Werte für das erste und zweite Element der Folge sind unterschiedlich.
Verallgemeinerte Fibonacci-Sequenz
Wir werden nun zeigen, dass unser Ansatz auch zur Berechnung beliebiger verallgemeinerter Fibonacci-Sequenzen geeignet ist. Die Fibonacci-Sequenz hängt von den beiden vorhergehenden Werten ab. Wir verallgemeinern dieses Konzept jetzt, indem wir eine k-Fib-Sequenz folgendermaßen definieren
Gegeben seien eine natürlichen Zahl k mit k >= 2 und k Anfangswerte
$i_0, i_1, \ldots i_{k-1}$ für die gilt $F_k(0) = i_0, \ldots F_k(k-1) = i_{k-1}$
Die Funktion benötigt auch $k$ Koeffizienten $c_0, c_1, \ldots c_{k-1}$
$ F_k(n)$ ist definiert als
$$ F_k(n) = a_0 \cdot F_k(n-1) + a_1 \cdot F_k(n-2) \ldots a_{k-1} \cdot F_k(n-k)$$mit $k <= n$
class kFibonacci:
def __init__(self, k, initials, coefficients):
self.memo = dict(zip(range(k), initials))
self.coeffs = coefficients
self.k = k
def __call__(self, n):
k = self.k
if n not in self.memo:
result = 0
for coeff, i in zip(self.coeffs, range(1, k+1)):
result += coeff * self.__call__(n-i)
self.memo[n] = result
return self.memo[n]
fib = kFibonacci(2, (0, 1), (1, 1))
lucas = kFibonacci(2, (2, 1), (1, 1))
for i in range(1, 16):
print(i, fib(i), lucas(i))
Die Folge der Pell-Nummern beginnt mit 1, 2, 5, 12, 29, ...
Die Funktion ist
$P(n) = 2 \cdot P(n-1) + P(n-2)$ mit $P(0) = 1$ und $P(1) = 1$
Es ist einfach, diese Sequenz mit unserer kFibonacci Klasse zu formulieren:
P = kFibonacci(2, (1, 2), (2, 1))
for i in range(10):
print(i, P(i))
Wir können eine weitere interessante Reihe erstellen, indem wir die Summe der beiden vorherigen Pell-Zahlen zwischen zwei Pell-Zahlen P (i) und P (i + 1) addieren. Wir bekommen:
$ P(0), P(1), P(0) + P(1), P(2), P(1) + P(2), P(3), P(2) + P(3) , \ldots $
korrespondierend zu: $ 1, 2, 3, 5, 7, 12, 17, 29, \ldots $
def nP(n):
if n < 2:
return P(n)
else:
i = n // 2 + 1
if n % 2: # n is odd
return P(i)
else:
return P(i-1) + P(i-2)
for i in range(20):
print(nP(i), end=", ")
Wenn Sie sich die Zahlen genau ansehen, sehen Sie, dass diese Reihenfolge eine andere Regel enthält. Wir können nP wie folgt definieren:
$nP(n) = 2 \cdot nP(n-2) + nP(n-4)$ mit $n > 3$ und den Startwerten $1, 2, 3, 5$
Dies ist eine weitere einfache Anwendung für unsere kFibonacci Klasse:
nP = kFibonacci(4, (1, 2, 3, 5), (0, 2, 0, 1))
for i in range(20):
print(nP(i), end=", ")
Eine interessante mathematische Tatsache: Für jedes ungerade n ist der Quotient von $P(n)$ durch $P(n-1) $ eine Annäherung an $\sqrt{2}$. Wenn n gerade ist, ist der Quotient eine Annäherung an $1 + {1 \over {\sqrt{2}}}$
qdwl2 = 2 ** 0.5
print("Quadratwurzel von 2: ", qdwl2)
print("Quadratwurzel von 3: ", 1 + 1 / qdwl2)
for i in range(1, 20):
print(nP(i) / nP(i-1), end=", ")
Weitere Informationen zur Rekursion in Python

Wenn Sie mehr über Rekursion erfahren möchten, empfehlen wir Ihnen, die folgenden Übungen zu lösen. Bitte schauen Sie sich die Lösungen nicht an, bevor Sie Ihr Bestes gegeben haben. Wenn Sie eine Weile über eine Aufgabe nachgedacht haben und die Übung immer noch nicht lösen können, dürfen Sie unsere Beispiellösungen konsultieren.
In unserem Abschnitt "Fortgeschrittene Themen" unseres Tutorials haben wir eine umfassende Beschreibung des Spiels oder Puzzles "Towers of Hanoi". Natürlich lösen wir es mit einer Funktion, die eine rekursive Funktion verwendet. Das "Hanoi-Problem" ist etwas Besonderes, da sich dem Programmierenden fast eine rekursive Lösung aufdrängt, während die iterative Lösung des Spiels schwer zu finden und zu begreifen ist.
Übungen
Übung 1
Überlegen Sie sich eine rekursive Version der Funktion $f(n) = 3 \cdot n$.
Übung 2
Schreiben Sie eine rekursive Python-Funktion, die die Summe der ersten n ganzen Zahlen zurückgibt. (Hinweis: Die Funktion ähnelt der Fakultätsfunktion!)
Übung 3
Schreiben Sie eine Funktion, die das Pascal-Dreieck implementiert:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
Übung 4
Die Fibonacci-Zahlen sind im Pascalschen Dreieck versteckt. Wenn Sie die farbigen Zahlen des folgenden Dreiecks ausummieren, erhalten Sie die 7. Fibonacci-Zahl:
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
Schreiben Sie ein rekursives Programm zur Berechnung der Fibonacci-Zahlen unter Verwendung des Pascal-Dreiecks.
Übung 5
Implementieren Sie in Python eine rekursive Funktion für das Sieb von Eratosthenes.
Das Eratosthenes-Sieb ist ein einfacher Algorithmus zum Ermitteln aller Primzahlen bis zu einer bestimmten Ganzzahl. Es wurde vom antiken griechischen Mathematiker Eratosthenes erfunden. Der Algorithmus zum Finden aller Primzahlen, die kleiner oder gleich einer gegebenen ganzen Zahl n sind lautet:
- Erstellen Sie eine Liste von Ganzzahlen von zwei bis n: 2, 3, 4, ..., n
- Beginnen Sie mit einem Zähler i, der auf 2 gesetzt ist, d.h. der ersten Primzahl
- Ausgehend von i + i zählen Sie bis i hoch und entfernen Sie diese Zahlen aus der Liste, d.h. 2 i, 3 i, 4 * i usw.
- Finden Sie die erste Zahl der Liste nach i. Dies ist die nächste Primzahl.
- Setzen Sie i auf die im vorherigen Schritt gefundene Zahl
- Wiederholen Sie die Schritte 3 und 4, bis i größer als n ist. (Als Verbesserung: Es reicht aus, zur Quadratwurzel von n zu gehen)
- Alle Zahlen, die noch in der Liste enthalten sind, sind Primzahlen
Sie können leicht erkennen, dass wir ineffizient wären, wenn wir diesen Algorithmus strikt verwenden würden, z. Wir werden versuchen, die Vielfachen von 4 zu entfernen, obwohl sie bereits durch die Vielfachen von 2 entfernt wurden. Es reicht also aus, die Vielfachen aller Primzahlen bis zur Quadratwurzel von n zu erzeugen. Wir können diese Mengen rekursiv erstellen.
Übung 6
Schreiben Sie eine rekursive Funktion fib_indexfib(), die den Index einer Zahl in der Fibonacci-Folge zurückgibt, wenn die Zahl ein Element dieser Folge ist, und -1 zurückgibt, wenn die Zahl nicht darin enthalten ist, d.h.
$fib(fib_index(n)) == n$
Übung 7
Die Summe der Quadrate zweier aufeinanderfolgender Fibonacci-Zahlen ist ebenfalls eine Fibonacci-Zahl, beispielsweise sind 2 und 3 Elemente der Fibonacci-Sequenz und 2 2 + 3 3 = 13 entspricht Fib (7). Verwenden Sie die vorherige Funktion, um die Position der Summe der Quadrate zweier aufeinanderfolgender Zahlen in der Fibonacci-Sequenz zu ermitteln.
Mathematische Erklärung:
Seien a und b zwei aufeinanderfolgende Fibonacci-Zahlen mit a vor b. Die Fibonacci-Sequenz, die mit der Zahl "a" beginnt, sieht folgendermaßen aus:
0 a
1 b
2 a + b
3 a + 2b
4 2a + 3b
5 3a + 5b
6 5a + 8b
Wir können sehen, dass die Fibonacci-Zahlen als Faktoren für a und b erscheinen. Das n-te Element in dieser Sequenz kann mit der folgenden Formel berechnet werden:
$F(n) = Fib(n-1) \cdot a + Fib(n) \cdot b$
Daraus können wir schließen, dass für eine natürliche Zahl n, n> 1 Folgendes gilt:
$Fib(2 \cdot n + 1) = Fib(n)^2 + Fib(n+1)^2$
Übung 8
Die Tribonacci-Zahlen sind wie die Fibonacci-Zahlen, aber anstatt mit zwei vorgegebenen Termen zu beginnen, beginnt die Sequenz mit drei vorbestimmten Termen und jeder Term danach ist die Summe der vorhergehenden drei Termen. Die ersten Tribonacci-Zahlen sind:
$ 0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, 927, 1705, 3136, 5768, 10609, 19513, 35890, 66012, \ldots $
Die Tetranacci-Zahlen beginnen mit vier vorgegebenen Termen, wobei jeder Termen danach die Summe der vorhergehenden vier Termen ist. Die ersten Tetranacci-Zahlen sind:
$0, 0, 0, 1, 1, 2, 4, 8, 15, 29, 56, 108, 208, 401, 773, 1490, 2872, 5536, 10671, 20569, 39648, \dots $
Dies wird auf die gleiche Weise für Pentanacci, Hexanacci, Heptanacci, Octanacci usw. fortgesetzt.
Schreiben Sie eine Funktion für die Tribonacci und Tetranacci Zahlen.
Übung 9:
Was ist, wenn jemand die Parameter in einer rekursiven Funktion überprüfen möchte? Zum Beispiel die Fakultätsfunktion. Okay, bitte schreiben Sie eine rekursive Version von Fakultät, die die Parameter überprüft. Vielleicht hast du es perfekt gemacht, aber vielleicht auch nicht. Können Sie Ihre Version verbessern? Unnötige Tests loswerden?
def mult3(n):
if n == 1:
return 3
else:
return mult3(n-1) + 3
for i in range(1,10):
print(mult3(i))
def sum_n(n):
if n== 0:
return 0
else:
return n + sum_n(n-1)
def pascal(n):
if n == 1:
return [1]
else:
Linie = [1]
previous_line = pascal(n-1)
for i in range(len(previous_line)-1):
line.append(previous_line[i] + previous_line[i+1])
line += [1]
return line
print(pascal(6))
Alternativ können wir eine Funktion mit Listenverständnis schreiben:
def pascal(n):
if n == 1:
return [1]
else:
p_line = pascal(n-1)
line = [ p_line[i]+p_line[i+1] for i in range(len(p_line)-1)]
line.insert(0,1)
line.append(1)
return line
print(pascal(6))
def fib_pascal(n,fib_pos):
if n == 1:
line = [1]
fib_sum = 1 if fib_pos == 0 else 0
else:
line = [1]
(previous_line, fib_sum) = fib_pascal(n-1, fib_pos+1)
for i in range(len(previous_line)-1):
line.append(previous_line[i] + previous_line[i+1])
line += [1]
if fib_pos < len(line):
fib_sum += line[fib_pos]
return (line, fib_sum)
def fib(n):
return fib_pascal(n,0)[1]
# and now printing out the first ten Fibonacci numbers:
for i in range(1,10):
print(fib(i))
from math import sqrt
def sieve(n):
# returns all primes between 2 and n
primes = list(range(2,n+1))
max = sqrt(n)
num = 2
while num < max:
i = num
while i <= n:
i += num
if i in primes:
primes.remove(i)
for j in primes:
if j > num:
num = j
break
return primes
print(sieve(100))
In diesem Kapitel unseres Tutorials geht es jedoch um Rekursion und rekursive Funktionen, und wir haben eine rekursive Funktion zur Berechnung der Primzahlen gefordert. Um die folgende Lösung zu verstehen, können Sie unser Kapitel über die List Comprehension zu Rate ziehen:
from math import sqrt
def primes(n):
if n == 0:
return []
elif n == 1:
return []
else:
p = primes(int(sqrt(n)))
no_p = [j for i in p for j in range(i*2, n + 1, i)]
p = [x for x in range(2, n + 1) if x not in no_p]
return p
print(primes(100))
memo = {0:0, 1:1}
def fib(n):
if not n in memo:
memo[n] = fib(n-1) + fib(n-2)
return memo[n]
def fib_index(*x):
""" findet die natürliche Zahl i mit fib (i) == n """
if len(x) == 1:
# vom Benutzer gestartet
# Index ab 0 finden
return fib_index(x[0], 0)
else:
n = fib(x[1])
m = x[0]
if n > m:
return -1
elif n == m:
return x[1]
else:
return fib_index(m, x[1]+1)
# Code aus dem vorherigen Beispiel mit den Funktionen fib() und find_index()
print(" index of a | a | b | sum of squares | index ")
print("=====================================================")
for i in range(15):
square = fib(i)**2 + fib(i+1)**2
print(f"{i:12d}|{fib(i):6d}|{fib(i+1):10d}|{square:14d}|{fib_index(square):5d}")
tribonacci = kFibonacci(3, (0, 0, 1), (1, 1, 1))
for i in range(20):
print(tribonacci(i), end=", ")
tetranacci = kFibonacci(4, (0, 0, 0, 1), (1, 1, 1, 1))
for i in range(20):
print(tetranacci(i), end=", ")
Wir können sie ganz einfach wie folgt erzeugen:
prefixes = ['tribo', 'tetra', 'pentra', 'hexa', 'hepta', 'octa']
for k, prefix in zip(range(len(prefixes)), prefixes):
cmd = prefix + "nacci = kFibonacci("
cmd += str(k+3) + ", (" + "0, " * (k+2) + "1), "
cmd += "(" + "1, " * (k+2) + "1))"
print(cmd)
exec(cmd)
print("\nEin Test der octanacci-Funktion: ")
for i in range(20):
print(octanacci(i), end=", ")
def Fakultät(n):
""" berechnet die Fakultät von n,
n sollte eine ganze Zahl sein und n <= 0 """
if type(n) == int and n >=0:
if n == 0:
return 1
else:
return n * Fakultät(n-1)
else:
raise TypeError("n muss eine positive ganze Zahl oder Null sein")
Was halten Sie von dieser Lösung? Wenn man Fakultät(10) aufruft, erfolgt automatisch ein Test, ob n, also 10, eine positive ganze Zahl ist. In der Funktion rufen wir dann n * Fakultät(n-1) auf. Wenn der Wert von n eine positive ganze Zahl ist, dann ist trivialerweise auch n-1 eine ganze Zahl. Dennoch wird unsere Funktion auch in diesem Fall und in allen anderen rekursiven Aufrufen, den Test unnötigerweise durchführen. Wir werden rekursiv Fakultät (9) nennen. wir werden noch einmal prüfen, ob 9 eine ganze Zahl ist. Was kann es noch sein? Wir hatten zuvor 10 überprüft und alles, was wir getan haben, war 1 zu subtrahieren.
Wir können dieses Problem überwinden, indem wir eine innere Funktion definieren:
def Fakultät(n):
""" berechnet die Fakultät von n,
n sollte eine ganze Zahl sein und n <= 0 """
def innere_Fakultät(n):
if n == 0:
return 1
else:
return n * innere_Fakultät(n-1)
if type(n) == int and n >=0:
return innere_Fakultät(n)
else:
raise TypeError("n sollte ein positives int oder 0 sein")
print(Fakultät(10))
Der Test wird nur beim ersten Anruf mit 10 durchgeführt!


 Buch kaufen
Buch kaufen
 Buch kaufen
Buch kaufen
 Buch kaufen
Buch kaufen


