Matrix-Arithmetik unter NumPy und Python

Verfremdeter Abbakus Im vorigen Kapitel unserer Einführung in NumPy zeigten wir, wie man Arrays erzeugen und ändern kann. In diesem Kapitel wollen wir zeigen, wie wir in Python mittels NumPy ohne Aufwand und effizient Matrizen-Arithmetic betreiben können, also



Die arithmetischen Standardoperationen werden elementweise angewendet, d.h. die Arrays müssen die gleichen Größen haben, damit man diese Operatoren anwenden kann. 
>>> x = np.array([1,5,2])
>>> y = np.array([7,4,1])
>>> x + y
array([8, 9, 3])
>>> x * y
array([ 7, 20,  2])
>>> x - y
array([-6,  1,  1])
>>> x / y
array([0, 1, 2])
>>> x % y
array([1, 1, 0])



Vektor-Addition und Vektor-Subtraktion

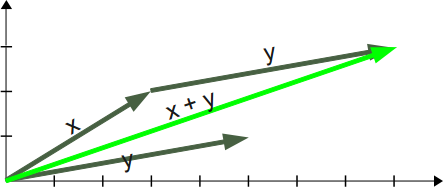Graphical Example of Vector Addition Vielen dürfte die Vektoraddition aus dem Physikunterricht der Schule bekannt sein. Man benutzt die Vektoraddition, um die Gesamtkraft zu berechnen, wenn verschiedene Einzelkräfte mit unterschiedlichen Ausrichtungen auf einen als punktförmig angenommenen Körper einwirken. Wenn man wissen will, welche Kraft insgesamt auf den Körper ausgeübt wird, muss man eine sogenannte Vektoraddition durchführen. Grafisch wird eine Vektoraddition realisiert, indem man durch Parallelverschiebung an die Spitze des ersten Vektors, also die Stelle, an der sich der Pfeil befindet, den Anfang des zweiten Vektors ansetzt.

Rechnerisch kann man mit der Vektoraddition die Gesamtverschiebung der Vektoren ermitteln, indem man die die jeweiligen Komponenten miteinander addiert. 
>>> x = np.array([3,2])
>>> y = np.array([5,1])
>>> z = x + y
>>> z
array([8, 3])
>>>
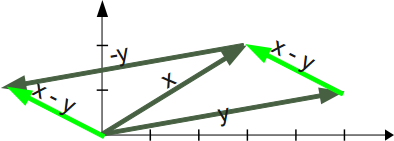Grafische Veranschulichung der Vektorsubtraktion Einen Vektor y von einem Vektor x zu subtrahieren ist das Gleiche wie wenn man das Negative von y zu dem Vektor x addiert.
Es gilt also:
x - y = x + (-y)
Geometrisch kann man die Subtraktion eines Vektors wie folgt durchführen: Um y von x zu subtrahieren plazieren wir die Endpunkte von x und y auf den gleichen Punkt. Dann zeichnen wir einen Pfeil von der Spitze von y zu der Spitze von x. Dieser "Pfeil" ist ein Repräsentant des Vektors x - y, siehe Bild auf der rechten Seite.

Mathematisch gesehen, wird die Vektorsubtraktion durch eine Komponentenweise Subtraktion der einzelnen Komponenten durchgeführt.

Skalarprodukt

Das Skalarprodukt wird häufig auch als Inneres Produkt oder Punktprodukt bezeichnet. Mathematisch stellt das Skalarprodukt eine algebraische Operation dar, die zwei Koordinationvektoren gleicher Größe als Argument nimmt und eine einfache Zahl zurückliefert. Das Ergebnis wird berechnet, indem die Komponenten mit gleichem Index multipliziert werden und die so erhaltenen Produkte anschließend addiert werden.
Der Name Punktprodukt (oder englisch "dot product") stammt übrigens davon, dass der "." häufig als Operatorzeichen für diese Operation genutzt wird. Der Name Skalarprodukt stellt mehr den Aspekt in den Vordergrund, dass das Ergebnis der Operation ein Skalar ist.

Definition des Skalarproduktes:

Definition des Skalarproduktes

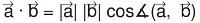
Aus der Definition des Skalarproduktes können wir ersehen, dass es benutzt werden kann, um den Winkel zwischen zwei Vektoren zu ermittlen.

Berechnung des Skalarproduktes:

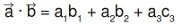
Skalarprodukt Berechnung

Im folgenden zeigen wir, wie man das Skalarprodukt mit Python und NumPy berechnet: 
>>> x = np.array([1,2,3])
>>> y = np.array([-7,8,9])
>>> np.dot(x,y)
36
>>> dot = np.dot(x,y)
>>> x_modulus = np.sqrt((x*x).sum())
>>> y_modulus = np.sqrt((y*y).sum())
>>> cos_angle = dot / x_modulus / y_modulus 
>>> angle = np.arccos(cos_angle) # Winkel in Bogenmaß
>>> angle  
0.80823378901082499
>>> angle * 360 / 2 / np.pi # Winkel in Gradmaß
46.308384970187326 	  	      
>>>

Matrix Klasse

Die Matrix-Klasse ist eine Unterklasse der NumPy-Arrays (ndarray). Ein Matrix-Objekt erbt alls Attribute und Methoden von ndarry. Ein Unterschied besteht darin, dass die NumPy-Matrizen streng 2-dimensional sind, während NumPy arrays von beliebiger Dimension sein können, also n-dimensional.

Der größte Vorteil von Matrizen liegt darin, dass sie eine komfortable Notation für verschiedene Matrizenoperationen, wie z.B. die Matrix-Multiplikation zur Verfügung stellen. Wenn X und Y zwei Matrizen sind, dann definiert X * Y die Matrixmultiplikation. Wenn allerdings X und Y zwei ndarrays sind, dann definiert X * Y eine Komponentenweise Multiplikation. 
>>> x = np.array( ((2,3), (3, 5)) )
>>> y = np.array( ((1,2), (5, -1)) )
>>> x * y
array([[ 2,  6],
       [15, -5]])
>>> x = np.matrix( ((2,3), (3, 5)) )
>>> y = np.matrix( ((1,2), (5, -1)) )
>>> x * y
matrix([[17,  1],
        [28,  1]])

Matrixprodukt

Das Matrixprodukt zweier Matrizen kann berechnet werden, wenn die Anzahl der Spalten der ersten Matrix gleich der Anzahl der Zeilen der zweiten Matrix ist.
Das Produkt einer (l x m)-Matrix A = (aij)i=1...l, j= 1..m und einer (m x n)-Matrix B = (bij)i=1...m, j= 1..n ist eine Matrix C = (cij)i=1...l, j= 1..n, die wie folgt berechnet wird:

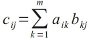
Matrix Product

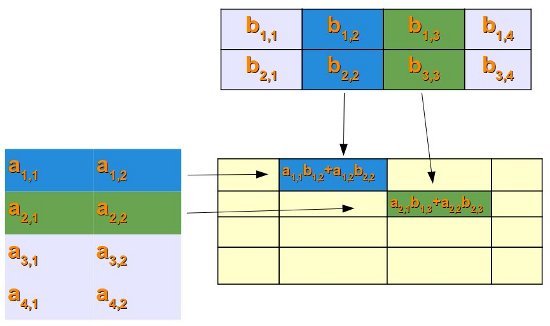
Die folgende Grafik verdeutlicht dieses Verfahren:
Illustration des Matrixproduktes

Wenn wir die Matrizenmultiplikation mit zwei NumPy Arrays (ndarray) durchführen wollen, müssen wir das Punktprodukt benutzen: 
>>> x = np.array( ((2,3), (3, 5)) )
>>> y = np.matrix( ((1,2), (5, -1)) )
>>> np.dot(x,y)
matrix([[17,  1],
        [28,  1]])
Alternativ können wir auch die Arrays ins Matrix Objekte casten und dann den "*"-Operator benutzen: 
>>> np.mat(x) * np.mat(y)
matrix([[17,  1],
        [28,  1]])

Eine einfache praktische Anwendung zum Matrizenprodukt

Pralinen In dem folgenden praktischen Beispiel kommen wir auf die Schokoladenseite des Lebens zu sprechen.
Nehmen wir an, wir haben vier Personen, die wir Lukas, Mia, Leon und Hannah taufen. Jeder von ihnen hat Pralinen der Marken A, B und C gekauft. Lukas kaufte 100 g der Marke A, 175 g der Marke B und 210 von C. Mia wählte 90 g von A, 160 g von B und 150 g von C. Leon kaufte 200 g von A, 50 von B und 100 g von C. Hannah mag allem Anschein nach nicht die Sorte B, weil sie keine Pralinen dieser Sorte gekauft hatte. Dafür scheint sie ein echter Fan der Sorte C zu sein, weil sie davon gleich 310 g gekauft hatte. Außerdem kaufte sie noch 120 g der Make A.

Nun wollen Sie natürlich wissen - oder auch nicht - wieviel die einzelnen Sorten kosten: A kostet 2.98 pro 100 g, B kostet 3.90 und C nur 1.99 Euro.

Wenn wir nun berechnen wollen wieviel jeder von ihnen zu zahlen hatte, können wir NumPy und die Matrizenmultiplikation nutzen: 

>>> PersAnz = np.array([[100,175,210],[90,160,150],[200,50,100],[120,0,310]])
>>> Preis_per_100_g = np.array([2.98,3.90,1.99])
>>> Preis_in_Cent = np.dot(PersAnz,Preis_per_100_g)
>>> Preis_in_  Euro = Preis_in_Cent / np.array([100,100,100,100])
>>> Preis_in_Euro
array([ 13.984,  11.907,   9.9  ,   9.745])
>>>
Das bedeutet, dass Lukas 13.98 Euro, Mia 11.97 Euro, Leon 9.90 und Hannah 9.75 zu zahlen hatte.

Kreuzprodukt / Vektorprodukt

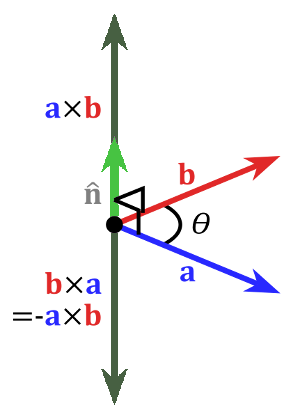Diagramm Kreuzprodukt So nun müssen wir wieder den Konsum der leckeren Pralinen einstellen und uns einem kalorienärmeren mathematischeren Thema zuwenden, dem Kreuzprodukt oder Vektorprodukt.

Das Kreuz- oder Vektorprodukt ist eine binäre Operation im dreidimensionalen Raum.
Das Kreuzprodukt zweier Vektoren a und b wird mit a × b bezeichnet.

Das Ergebnis ist ein Vektor, der senkrecht zu den Vektoren steht, die multipliziert werden. Senkrecht im Sinne eines Rechtssystems, d.h. die beiden Vektoren a und b sowie a x b verhalten sich wie Daumen, Zeigefinger und Mittelfinger der rechten Hand (sogenannte Drei-Finger-Regel).

Das Kreuzprodukt ist definiert als:
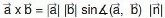
Definition des Kreuzproduktes
wobei n ein Einheitsvektor ist, der senkrecht auf der von a und b aufgespannten Ebene steht. Es gibt zwei Vektoren, die diese Eigenschaft erfüllen. Der richtige ist der, der mit der Drei- Finger-Regel (siehe oben) ermittelt werden kann.

Falls einer der Vektoren, die multipliziert werden Null ist oder wenn die beiden Vektoren parallel sind, dann ist ihr Kreuzprodukt gleich Null. Die Länge des Ergebnisvektors entspricht der Fläche des von den beiden multiplizierten Vektoren aufgespannten Parallelogrammes. Falls die beiden Vektoren senkrecht zueinander stehen, erhalten wir ein Rechteck. 

>>> x = np.array([0,0,1])
>>> y = np.array([0,1,0])

>>> np.cross(x,y)
array([-1,  0,  0])

>>> np.cross(y,x)
array([1, 0, 0])