# invisible
import numpy as np
np.core.arrayprint._line_width = 65

Dimensionsänderungen


Tesserakt

Bisher lernten wir, wie man Arrays erzeugt und wie wir numerische Operationen auf NumPy Arrays anwenden können. Wenn wir mit NumPy programmieren, kommen wir früher oder später zu dem Punkt, wo wir Funktionen benötigen, um die Gestalt (shape) und die Dimension von Arrays zu manipulieren. Die dazu nötigen Funktionalitäten lernen wir in diesem Kapitel kennen. Wir werden auch lernen, wie man Arrays zusammenhängt bzw. konkateniert. Weiterhin werden wir die Möglichkeiten demonstrieren, wie man weitere Dimensionen an existierende Arrays anhängen kann und wie man mehrere Arrays horizontal und vertikal "stapeln" (stack) kann. Dieses Kapitel beenden wir, indem wir zeigen, wie man neue Arrays durch Wiederholungen aus existierenden Arrays erzeugen kann.

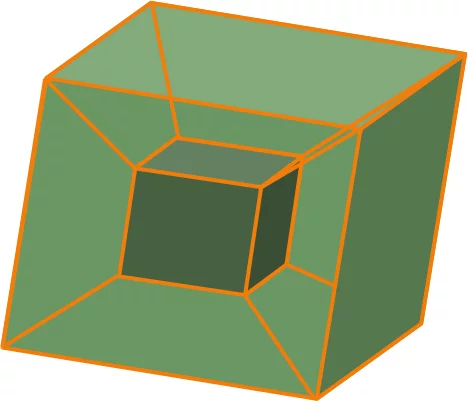
Das Bild zeigt einen Tesserakt, den man auch als vierdimensionalen Hyperwürfel bezeichnet. Ein Tesserakt kann man als die Übertragung des Konzeptes eines dreimensionalen Würfels in den vierdimensionalen Raum sehen. Ein Tesserakt verhält sich zum Würfel wie ein Würfel zum Quadrat.

Reduktion und Reshape von Arrays

Es gibt mehrere Methoden, um ein multidimensionales Array zu reduzieren:

  • flatten
  • ravel
  • reshape

flatten

flatten ist eine ndarray-Methode mit einem optionalen Parameter order, der die Werte C, F und A annehmen kann. Der Default-Wert von order ist C.
C steht dafür, dass im C-Stil in der Zeilen-Haupt-Ordnung linearisiert bzw. flach gemacht wird, d.h. der am weitesten rechts liegende Index "ändert sich am schnellsten". In anderen Worten: Der Zeilenindex variiert in der Zeilen-Haupt-Ordnung am langsamsten und am Spaltenindex am schnellsten, sodass a[0, 1] auf a[0, 0] folgt.
F steht für "Fortran Spalten-Haupt-Ordnung".
A steht für den Erhalt der "C/Fortran-Anordnung".

import numpy as np
A = np.array([[[ 0,  1],
               [ 2,  3],
               [ 4,  5],
               [ 6,  7]],
              [[ 8,  9],
               [10, 11],
               [12, 13],
               [14, 15]],
              [[16, 17],
               [18, 19],
               [20, 21],
               [22, 23]]])
Flattened_X = A.flatten()
print(Flattened_X)
print(A.flatten(order="C"))
print(A.flatten(order="F"))
print(A.flatten(order="A"))

[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
[ 0  8 16  2 10 18  4 12 20  6 14 22  1  9 17  3 11 19  5 13 21  7 15 23]
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]

ravel

Die Reihenfolge der Elemente, die durch ravel() zurückgeliefert wird, ist standardmäßig im "C-Stil".

ravel(X, order='C')

ravel erzeugt ein linearisiertes, also eindimensionales, Array . Eine Kopie wird nur bei Notwendigkeit erstellt.

Der optionale Parameter order kann die Werte C, F, A oder K annehmen.

C: C-Stil Reihenfolge, wobei sich der letzte Achsenindex am schnellsten ändert, zurück zum ersten Achsenindex, der sich am langsamsten ändert. C ist der Default-Wert.

F: Fortran-Stil Indexreihenfolge, wobei sich der erste Index am schnellsten ändert und der letzte Index am langsamsten.

A: Fortran-Stil Indexreihenfolge, wenn das Array 'a' im Speicher als Fortran vorliegt, andernfalls wird die C-Stil Reihenfolge verwendet.

K: Die Elemente werden so gelesen, wie sie im Speicher vorkommen, außer für Datenumkehrung, wenn die Schrittweiten negativ sind.

print(A.ravel())
print(A.ravel(order="A"))
print(A.ravel(order="F"))
print(A.ravel(order="A"))
print(A.ravel(order="K"))

[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
[ 0  8 16  2 10 18  4 12 20  6 14 22  1  9 17  3 11 19  5 13 21  7 15 23]
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]

Unterschiede zwischen ravel und flatten

  • ravel liefert in der Regel keine Kopie, sondern eine auf die Dimension angepasste View auf das Originalarray zurück.
  • flatten liefert immer eine Kopie zurück.
  • ravel ist schneller als flatten, weil es keine Kopie erzeugen muss.

Wir zeigen dies in Beispielen:

import numpy as np
A = np.array([[1, 2, 3],
              [4, 5, 6]])
B = A.flatten()
B[4] = 42
print("B: \n", B)
print("A: \n", A)
print(np.may_share_memory(A, B))
print("\n... und jetzt das Ganze mit ravel:")
B = A.ravel()
B[4] = 42
print("B: \n", B)
print("A: \n", A)
print(np.may_share_memory(A, B))

B: 
 [ 1  2  3  4 42  6]
A: 
 [[1 2 3]
 [4 5 6]]
False
... und jetzt das Ganze mit ravel:
B: 
 [ 1  2  3  4 42  6]
A: 
 [[ 1  2  3]
 [ 4 42  6]]
True

reshape

Die reshape-Methode wandelt ein Array in eine neue Gestalt, englisch ,,Shape'', ohne die darin enthaltenen Daten zu ändern, d.h. die eigentlichen Daten müssen nicht kopiert werden.

reshape(a, newshape, order='C')

Parameter Bedeutung
a array-ähnlich, Array, das geändert werden soll.
newshape Integer-Wert oder Integer-Tupel
order 'C', 'F', 'A', wie in flatten() oder ravel()

Mittels reshape können wir ein Array auch linearisieren:

A = np.array([[1, 2, 3],
              [4, 5, 6]])
B = A.reshape((6,))
print(B)

[1 2 3 4 5 6]

Damit kann reshape die Aufgaben von ravel und flatten übernehmen. reshape kann aber noch mehr. Wir können damit ein Array A in eine beliebige Gestalt x überführen, solange das Produkt der Shape-Komponenten von A gleich dem Produkt der Shape-Komponenten von x ist, also

np.prod(A.shape) == np.prod(x)

X = np.array(range(24))
Y1 = X.reshape((3, 4, 2))
print(Y1)
new_shape = (2, 3, 4)
Y2 = Y1.reshape(new_shape)
print(Y2)

[[[ 0  1]
  [ 2  3]
  [ 4  5]
  [ 6  7]]
 [[ 8  9]
  [10 11]
  [12 13]
  [14 15]]
 [[16 17]
  [18 19]
  [20 21]
  [22 23]]]
[[[ 0  1  2  3]
  [ 4  5  6  7]
  [ 8  9 10 11]]
 [[12 13 14 15]
  [16 17 18 19]
  [20 21 22 23]]]

Es gilt:

np.prod(Y1.shape) == np.prod(new_shape)
Ausgabe: :

True


Konkatenation von Arrays

Im folgenden Beispiel konkatenieren wir drei eindimensionale Arrays zu einem. Die Elemente des zweiten Arrays werden an das erste Array horizontal angefügt. Anschließend werden die Elemente des dritten Arrays ebenfalls horizontal angefügt:

x = np.array([11, 22])
y = np.array([18, 7, 6])
z = np.array([1, 3, 5])
c = np.concatenate((x, y, z))
print(c)

[11 22 18  7  6  1  3  5]

Wenn wir multidimensionale Arrays zusammenführen, müssen wir auf die Achsen achten. Die Arrays müssen die gleiche Shape haben, um mit concatenate zusammen gefügt werden zu können. Bei multidimensionalen Arrays können wir diese entsprechend anordnen. Der Default-Wert ist axis = 0:

x = np.array(range(12))
x = x.reshape((3, 4))
y = np.array(range(100, 112))
y = y.reshape((3, 4))
z = np.concatenate((x, y))
print(z)

[[  0   1   2   3]
 [  4   5   6   7]
 [  8   9  10  11]
 [100 101 102 103]
 [104 105 106 107]
 [108 109 110 111]]

Wir führen die Zusammenführung nun mit axis = 1 durch:

z = np.concatenate((x, y), axis=1)
print(z)

[[  0   1   2   3 100 101 102 103]
 [  4   5   6   7 104 105 106 107]
 [  8   9  10  11 108 109 110 111]]


Weitere Dimensionen hinzufügen

Weitere Dimensionen können zu einem Array mit Hilfe von Slicing und np.newaxis hinzugefügt werden. Wir demonstrieren die Technik im folgenden Beispiel:

x = np.array([2,5,18,14,4])
y = x[:, np.newaxis]
print(y)

[[ 2]
 [ 5]
 [18]
 [14]
 [ 4]]

Das gleiche Resultat lässt sich auch mit reshape bewerkstelligen:

x = np.array([2,5,18,14,4])
y = x.reshape( (x.shape[0], 1) )
print(y)

[[ 2]
 [ 5]
 [18]
 [14]
 [ 4]]



Vektoren stapeln

A = np.array([[3, 4, 5]])
B = np.array([[1,9,0]])
C = np.dstack((A, B))
print("Elemente von A:")
for i in range(C.shape[1]):
    print(C[0, i, 0], end=", ")
print("\nElemente von B:")
for i in range(C.shape[1]):
    print(C[0, i, 1], end=", ")

Elemente von A:
3, 4, 5, 
Elemente von B:
1, 9, 0,

Wir können sehen, dass wir den i-ten Eingabevektor von C erhalten, indem wir den Ausdruck C[:, :, i] ausführen:

print("Erster Eingabevektor, d.h. A:", C[:, :, 0])
print("Zweiter Eingabevektor, d.h. B:", C[:, :, 1])

Erster Eingabevektor, d.h. A: [[3 4 5]]
Zweiter Eingabevektor, d.h. B: [[1 9 0]]

Als Nächstes betrachten wir die Methoden row_stack und column_stack:

A = np.array([3, 4, 5])
B = np.array([1,9,0])
print(np.row_stack((A, B)))
print(np.column_stack((A, B)))
print(np.shape(A))

[[3 4 5]
 [1 9 0]]
[[3 1]
 [4 9]
 [5 0]]
(3,)

A = np.array([[1, 2],
              [3, 4]])
X = np.column_stack((A, A, A))
print(np.row_stack((X, X, X)))     

[[1 2 1 2 1 2]
 [3 4 3 4 3 4]
 [1 2 1 2 1 2]
 [3 4 3 4 3 4]
 [1 2 1 2 1 2]
 [3 4 3 4 3 4]]



"Fliesen" mit "tile"

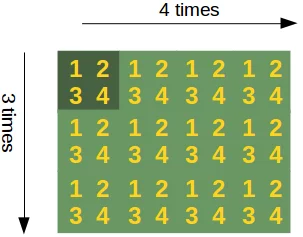
Manchmal ist es nötig, eine Matrix zu erstellen (mit einer anderen Shape oder Dimension), die den Inhalt einer existierenden Matrix mehrfach enthält.

Beispiel:

Man möchte das eindimensionale Array array([ 3.4]) in das Array array([ 3.4, 3.4, 3.4, 3.4, 3.4]) wandeln.

Weiteres Beispiel:

Man möchte ein zweidimensionales Array, wie np.array([ [1, 2], [3, 4]]), als Baustein benutzen, um ein Array mit der Shape (6, 8) zu erstellen:

array([[1, 2, 1, 2, 1, 2, 1, 2],
       [3, 4, 3, 4, 3, 4, 3, 4],
       [1, 2, 1, 2, 1, 2, 1, 2],
       [3, 4, 3, 4, 3, 4, 3, 4],
       [1, 2, 1, 2, 1, 2, 1, 2],
       [3, 4, 3, 4, 3, 4, 3, 4]])

Die Konstruktionsidee ist im folgenden Diagramm dargestellt:

Arbeitsweise der Tile-Methode


import numpy as np
x = np.array([ [1, 2], [3, 4]])
print(np.tile(x, (3, 4)))

[[1 2 1 2 1 2 1 2]
 [3 4 3 4 3 4 3 4]
 [1 2 1 2 1 2 1 2]
 [3 4 3 4 3 4 3 4]
 [1 2 1 2 1 2 1 2]
 [3 4 3 4 3 4 3 4]]

import numpy as np
x = np.array([ 3.4])
y = np.tile(x, (5,)) 
print(y)

[3.4 3.4 3.4 3.4 3.4]

Im vorigen tile-Beispiel hätten wir ebenso y = np.tile(x, 5) schreiben können.

Wenn wir reps in Tupel- oder List-Form schreiben, oder reps = 5 als Ersatz für reps = (5,) in Erwägung ziehen, so ist Folgendes wahr:

Wenn reps die Länge n hat, so wird die Dimension des resultierenden Arrays maximal n und A.ndim sein.

Wenn A.ndim < n ist, so wird A durch Voranstellen neuer Achsen auf die n-Dimensionen befördert. Beispielsweise wird ein Array mit der Shape (5,) auf (1, 5) bei einer 2-D-Replikation befördert oder auf die Shape (1, 1, 5) bei einer 3-D-Replikation. Sollte das nicht dem gewünschten Verhalten entsprechen, so ist A vor dem Aufruf der tile-Funktion auf die gewünschte Shape anzupassen.

Wenn A.ndim > d ist, so wird reps auf A.ndim angepasst, indem 1's vorangestellt werden. Beispielsweise wird ein Array A mit der Shape (2, 3, 4, 5) und reps = (2, 2) als (1, 1, 2, 2) behandelt.

Weitere Beispiele:

import numpy as np
x = np.array([[1, 2], [3, 4]])
print(np.tile(x, 2))

[[1 2 1 2]
 [3 4 3 4]]

import numpy as np
x = np.array([[1, 2], [3, 4]])
print(np.tile(x, (2, 1)))

[[1 2]
 [3 4]
 [1 2]
 [3 4]]

import numpy as np
x = np.array([[1, 2], [3, 4]])
print(np.tile(x, (2, 2)))

[[1 2 1 2]
 [3 4 3 4]
 [1 2 1 2]
 [3 4 3 4]]